
【题目】已知![]() ,
,![]() 均为奇函数,且
均为奇函数,且![]() 在
在![]() 上的最大值为
上的最大值为![]() ,则在
,则在![]() 上
上![]() 的最小值为__________.
的最小值为__________.
【答案】-1
【解析】
根据定义得出f(﹣x)+f(x)=0,g(﹣x)+g(x)=0,即F(x)+F(﹣x)=4,根据F(x)图象关于(0,2)对称,求解得出F(x)在(﹣∞,0)上的最小值F(﹣x0)=4﹣5=﹣1.
∵f(x)和g(x)都是定义域在R上的奇函数,若F(x)=af(x)+bg(x)+2,
则F(x)﹣2=af(x)+bg(x)为奇函数,
∵f(﹣x)+f(x)=0,g(﹣x)+g(x)=0,
∴F(x)+F(﹣x)=4,
F(x)图象关于(0,2)对称,
∵在(0,+∞)上有最大值为5,
∴最大值为F(x0)=5,
即F(x)在(﹣∞,0)上的最小值F(﹣x0)=4﹣5=﹣1.
故F(x)在(﹣∞,0)上的最小值为﹣1,
故答案为:﹣1


科目:高中数学 来源: 题型:
【题目】某兴趣小组进行“野岛生存”实践活动,他们设置了![]() 个取水敞口箱.其中
个取水敞口箱.其中![]() 个采用
个采用![]() 种取水法,
种取水法,![]() 个采用
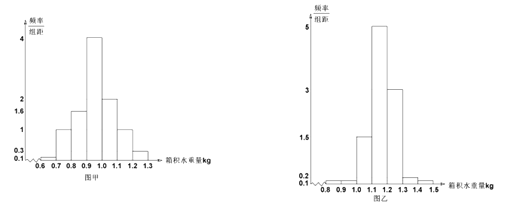
个采用![]() 种取水法.如图甲为
种取水法.如图甲为![]() 种方法一个夜晚操作一次
种方法一个夜晚操作一次![]() 个水箱积取淡水量频率分布直方图,图乙为
个水箱积取淡水量频率分布直方图,图乙为![]() 种方法一个夜晚操作一次
种方法一个夜晚操作一次![]() 个水箱积取淡水量频率分布直方图.
个水箱积取淡水量频率分布直方图.
(1)设两种取水方法互不影响,设![]() 表示事件“
表示事件“![]() 法取水箱水量不低于
法取水箱水量不低于![]() ,
,![]() 法取水箱水量不低于
法取水箱水量不低于![]() ”,以样本估计总体,以频率分布直方图中的频率为概率,估计
”,以样本估计总体,以频率分布直方图中的频率为概率,估计![]() 的概率;
的概率;
(2)填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为箱积水量与取水方法有关.
的把握认为箱积水量与取水方法有关.
箱积水量 | 箱积水量 | 箱数总计 | |
| |||
| |||
箱数总计 |
附:![]()
![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
B. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
C. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
D. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:


(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数分布直方图;
(3)若成绩在75.585.5分的学生为二等奖,问获得二等奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]()
![]() 一段图象如图所示。
一段图象如图所示。

(1)求出函数![]() 的解析式;
的解析式;
(2) 函数![]() 的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到?
的图像可由函数y=sinx的图像经过怎样的平移和伸缩变换而得到?
(3) 求出![]() 的单调递增区间;
的单调递增区间;
(4) 指出当![]() 取得最小值时
取得最小值时![]() 的集合.
的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加![]() 元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费
元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费![]() 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费![]() 元.
元.
(1)当每辆车的月租金定为![]() 元时,能租出多少辆车?
元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com