(本题满分15分)定义在
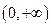
上的函数
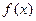
,对任意的
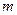
,
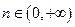
都有
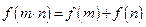
成立,且当
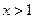
时,
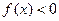
.
(1)试求
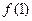
的值;
(2)证明:
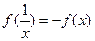
对任意
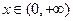
都成立;
(3)证明:
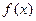
在
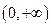
上是减函数;
(4)当
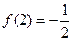
时,解不等式
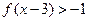
.
(1)0
(2)证明略
(3)证明略
(4)
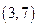
(1)∵
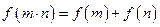
对任意的
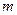
,
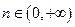
都成立,
∴令
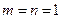
得,
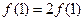
∴
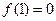
…….3分
(2)由题意及(1)可知,
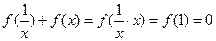
∴
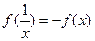
….6分
(3)证明:任取
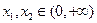
,且
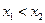
,
则
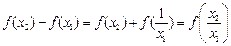
,
且
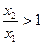
, 而当
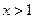
时,
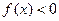
∴
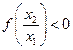
,
即
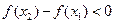
∴
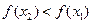
,
即函数
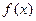
在
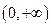
上是减函数;…….10分
(4)当
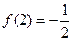
时,
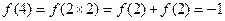
∴原不等式可化为
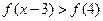
由(3)知,
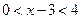
解得
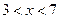
∴原不等式

的解集为
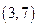
……15分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)
若f(x)是定义在(0,+
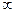
)上的增函数,且

⑴求f(1)的值;
⑵若f(6)=1,解不等式f(x+3)-f(
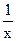
)<2.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设
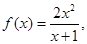
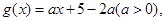
若对于任意
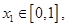
总存在
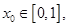
使得
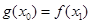
成立,则
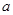
的取值范围是 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)
已知
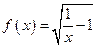
.
(1)求函数
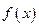
的定义域;
(2)判断并用定义证明函数
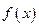
的单调性;
(3)求函数
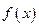
的反函数.
查看答案和解析>>

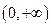 上的函数
上的函数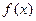 ,对任意的
,对任意的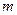 ,
,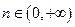 都有
都有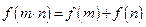 成立,且当
成立,且当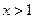 时,
时,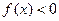 .
. 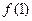 的值;
的值;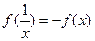 对任意
对任意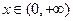 都成立;
都成立;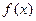 在
在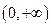 上是减函数;
上是减函数;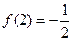 时,解不等式
时,解不等式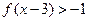 .
. 阅读快车系列答案
阅读快车系列答案