
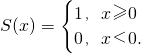 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).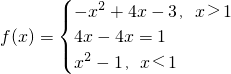 …(2分)
…(2分)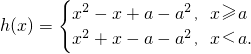
 时,h(x)在区间
时,h(x)在区间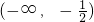 上单调递减,在区间
上单调递减,在区间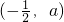 上单调递增,在区间(a,+∞)上单调递增.
上单调递增,在区间(a,+∞)上单调递增.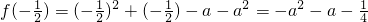 .…(6分)
.…(6分)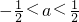 时,h(x)在区间
时,h(x)在区间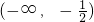 上单调递减,在区间
上单调递减,在区间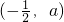 上单调递增,在区间
上单调递增,在区间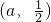 上单调递减,在区间
上单调递减,在区间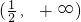 上单调递增.
上单调递增.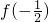 与
与 中较小的一个,即
中较小的一个,即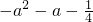 与
与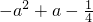 中较小的一个.
中较小的一个.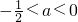 时,h(x)的最小值为
时,h(x)的最小值为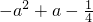 .…(7分)
.…(7分)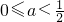 时,h(x)的最小值为
时,h(x)的最小值为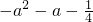 .…(8分)
.…(8分)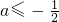 时,在区间(-∞,a)上单调递减,在区间
时,在区间(-∞,a)上单调递减,在区间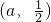 上单调递减,在区间
上单调递减,在区间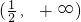 上单调递增.
上单调递增.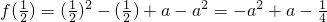 .…(9分)
.…(9分)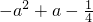 ,当a>0时,h(x)的最小值为
,当a>0时,h(x)的最小值为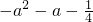 .…(10分)
.…(10分)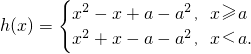 ,再结合二次函数的图象与性质,分a≥
,再结合二次函数的图象与性质,分a≥ 、0≤a<
、0≤a< 、-
、- <a<0和a≤-
<a<0和a≤- 的4种情况进行讨论,最后综合可得当a≤0时,h(x)的最小值为
的4种情况进行讨论,最后综合可得当a≤0时,h(x)的最小值为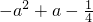 ;当a>0时,h(x)的最小值为
;当a>0时,h(x)的最小值为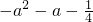 .
.

科目:高中数学 来源: 题型:解答题
 .
.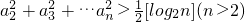 ;
;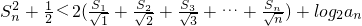 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 与
与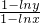 的大小.
的大小.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
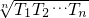 为“叠乘积”.如果有1618项的正项数列a1,a2,…,a1618的“叠乘积”为21619,则有1619项数列2,a1,a2,…,a1618…的“叠乘积”为
为“叠乘积”.如果有1618项的正项数列a1,a2,…,a1618的“叠乘积”为21619,则有1619项数列2,a1,a2,…,a1618…的“叠乘积”为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com