
【题目】已知数列![]() 满足
满足![]() 。
。
(1)若![]() 成等比数列,求
成等比数列,求![]() 的值。
的值。
(2)是否存在![]() ,使数列
,使数列![]() 为等差数列?若存在,求出所有这样的
为等差数列?若存在,求出所有这样的![]() ;若不存在,说明理由。
;若不存在,说明理由。
【答案】(1)![]() 或
或![]() ;(2) 当且仅当
;(2) 当且仅当![]() 时,数列
时,数列![]() 为等差数列.
为等差数列.
【解析】
试题(1)把![]() 表示为
表示为![]() 的式子,通过对
的式子,通过对![]() 的范围进行讨论去掉绝对值符号,根据
的范围进行讨论去掉绝对值符号,根据![]() 成等比数列可得关于
成等比数列可得关于![]() 的方程,解出即可;
的方程,解出即可;
(2)假设这样的等差数列存在,则![]() 成等差数列,即
成等差数列,即![]() ,将(1)的过程代入,得到关于
,将(1)的过程代入,得到关于![]() 的方程,分情况①当
的方程,分情况①当![]() 时②当
时②当![]() 时,求得
时,求得![]() 进行判断;看是否与
进行判断;看是否与![]() 矛盾.此题的难点在与讨论绝对值的几何意义,去绝对值.
矛盾.此题的难点在与讨论绝对值的几何意义,去绝对值.
试题解析:(1)∵![]() ,∴
,∴![]() ,
,![]() .
.
(ⅰ)当![]() 时,
时,![]() ,
,
由![]() ,
,![]() ,
,![]() 成等比数列得:
成等比数列得:
∴![]() ,解得
,解得![]() . 3分
. 3分
(ⅱ)当![]() 时,
时,![]()
∴![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() .
.
综上可得![]() 或
或![]() . 6分
. 6分
(2)假设这样的等差数列存在,则
由![]() ,得
,得![]() ,即
,即![]() .
.
(ⅰ)当![]() 时,
时,![]() ,解得
,解得![]() ,从而
,从而![]() (
(![]() ),此时
),此时![]() 是一个等差数列; 9分
是一个等差数列; 9分
(ⅱ)当![]() 时,
时,![]() ,解得
,解得![]() ,与
,与![]() 矛盾;
矛盾;
综上可知,当且仅当![]() 时,数列
时,数列![]() 为等差数列. 12分
为等差数列. 12分


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学基本公式大赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
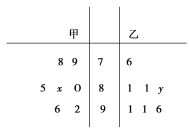
(1)求x和y的值;
(2)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设整数![]() ,对置于
,对置于![]() 个点
个点![]() 及点
及点![]() 处的卡片作如下操作:操作
处的卡片作如下操作:操作![]() :若某个点
:若某个点![]() 处的卡片数不少于3,则可从中取出三张,在三点
处的卡片数不少于3,则可从中取出三张,在三点![]() 、
、![]() 、
、![]() 处各放一张
处各放一张![]() ;操作
;操作![]() :若点
:若点![]() 处的卡片数不少于
处的卡片数不少于![]() ,则可从中取出
,则可从中取出![]() 张,在
张,在![]() 个点
个点![]() 处各放一张。证明:只要放置于这
处各放一张。证明:只要放置于这![]() 个点处的卡片总数不少于
个点处的卡片总数不少于![]() ,则总能通过若干次操作,使得每个点处的卡片数均不少于
,则总能通过若干次操作,使得每个点处的卡片数均不少于![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4,5这六个数字,完成下面三个小题.
(1)若数字允许重复,可以组成多少个不同的五位偶数;
(2)若数字不允许重复,可以组成多少个能被5整除的且百位数字不是3的不同的五位数;
(3)若直线方程![]() 中的a,b可以从已知的六个数字中任取2个不同的数字,则直线方程表示的不同直线共有多少条?
中的a,b可以从已知的六个数字中任取2个不同的数字,则直线方程表示的不同直线共有多少条?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an+1+(-1)n an =2n-1,则{an}的前64项和为( )
A. 4290 B. 4160 C. 2145 D. 2080
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.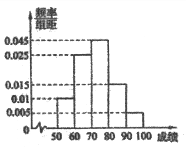
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com