Question

【题目】已知椭圆E: 的焦点在 轴上，A是E的左顶点，斜率为k(k>0)的直线交E于A,M两点，点N在E上，MA⊥NA.
（1）当t=4， 时，求△AMN的面积；
（2）当 时，求k的取值范围.

Answer 1

【答案】
（1）

解：当 时，椭圆E的方程为 ，A点坐标为 ，

则直线AM的方程为 ．

联立 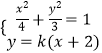并整理得，

解得 或 ，则

因为 ，所以

因为 ， ，

所以 ，整理得 ，

无实根，所以 ．

所以 的面积为

（2）

解：直线AM的方程为 ，

联立 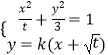并整理得，

解得 或 ，

所以

所以

因为

所以 ，整理得， ．

因为椭圆E的焦点在x轴，所以 ，即 ，整理得

解得

【解析】（1）求出t=4时，椭圆方程和顶点A，设出直线AM的方程，代入椭圆方程，求交点M，运用弦长公式求得|AM|，由垂直的条件可得|AN|，再由|AM|=|AN|，解得k=1，运用三角形的面积公式可得△AMN的面积；（2）直线AM的方程为y=k（x+ ），代入椭圆方程，求得交点M，可得|AM|，|AN|，再由2|AM|=|AN|，求得t，再由椭圆的性质可得t＞3，解不等式即可得到所求范围．