
 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 . 科目:高中数学 来源:2005-2006学年江苏省常州市武进区前黄高中高二(上)期末数学试卷(解析版) 题型:填空题
 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .查看答案和解析>>
科目:高中数学 来源:2011年高中数学综合测试卷(选修1-1)(解析版) 题型:填空题
 与双曲线
与双曲线 (m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 .
(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 .查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:圆锥曲线(2)(解析版) 题型:选择题
 与双曲线
与双曲线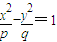 (m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )
(m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )查看答案和解析>>
科目:高中数学 来源:2010年高考考前数学客观题训练2(理科)(解析版) 题型:选择题
 与双曲线
与双曲线 (m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )
(m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com