
(本题满分14分)已知函数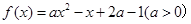
(Ⅰ)设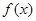 在区间
在区间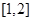 的最小值为
的最小值为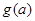 ,求
,求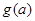 的表达式;
的表达式;
(Ⅱ)设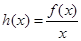 ,若函数
,若函数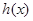 在区间
在区间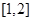 上是增函数,求实数
上是增函数,求实数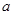 的取值范围。
的取值范围。
(1) 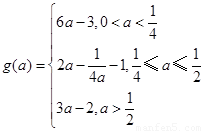 ;(2)
;(2)  ;
;
【解析】
试题分析:(1)由于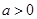 ,当
,当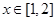 时,
时,
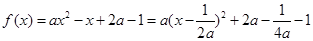 (1分)
(1分)
当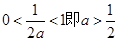 时,
时, 在
在 上为增函数,
上为增函数,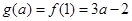 ;(3分)
;(3分)
当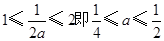 时,
时, 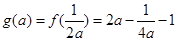 ;(5分)
;(5分)
当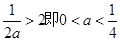 时,
时, 在
在 上为减函数,
上为减函数,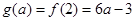 .(7分)
.(7分)
综上可得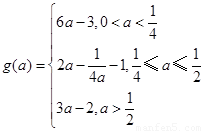 (8分)
(8分)
(2)  ,在区间[1,2]上任取
,在区间[1,2]上任取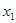 、
、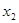 ,且
,且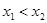
则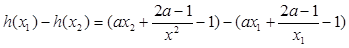
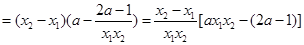 (*)(10分)
(*)(10分)
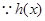 在
在 上为增函数,
上为增函数,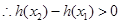
∴(*)可转化为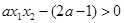 对任意
对任意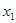 、
、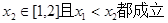
即 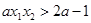 (12分)
(12分)
因为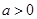 ,所以
,所以 ,由
,由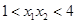 得
得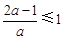 ,解得
,解得 ;
;
所以实数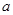 的取值范围是
的取值范围是 (14分)
(14分)
(2)另解: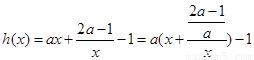
由于对勾函数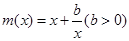 在区间
在区间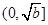 上递减,在区间
上递减,在区间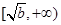 上递增;
上递增;
(10分)
∴当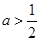 时,
时, ,由题应有
,由题应有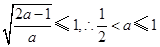 (12分)
(12分)
当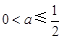 时
时 为增函数满足条件。
为增函数满足条件。
故实数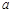 的取值范围是
的取值范围是 (14分)
(14分)
考点:本题考查了函数最值的求法及单调性的运用
点评:二次函数在闭区间上的最值受制于对称轴与区间的相对位置关系,特别是含参数的两类“定区间动轴、定轴动区间”的最值问题,要考察区间与对称轴的相对位置关系,分类讨论常成为解题的通法.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:2012-2013学年吉林省高三第一次月考文科数学试卷(解析版) 题型:解答题
(本题满分14分)已知函数
(1)若 ,求x的值;
,求x的值;
(2)若 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学理卷 题型:解答题
(本题满分14分)
已知椭圆 :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若动圆 与椭圆
与椭圆 和直线
和直线 都没有公共点,试求
都没有公共点,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学理卷 题型:解答题
((本题满分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
(1)当x=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,
,
求 的最大值;
的最大值;


(3)当 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com