
【题目】函数y=log ![]() cos(
cos( ![]() ﹣2x)的递增区间是 ( )
﹣2x)的递增区间是 ( )
A.[﹣ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
B.[﹣ ![]() +kπ,kπ)(k∈Z)
+kπ,kπ)(k∈Z)
C.[ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
D.[ ![]() +kπ,
+kπ, ![]() +kπ)(k∈Z)
+kπ)(k∈Z)
【答案】B
【解析】解:y=log ![]() cos(
cos( ![]() ﹣2x)=log
﹣2x)=log ![]() (﹣sin2x), 由﹣sin2x>0得sin2x<0,即2kπ﹣π<2x<2kπ,k∈Z,
(﹣sin2x), 由﹣sin2x>0得sin2x<0,即2kπ﹣π<2x<2kπ,k∈Z,
即kπ﹣ ![]() <x<kπ,k∈Z,
<x<kπ,k∈Z,
设t=﹣sin2x,则y=log ![]() t为减函数,
t为减函数,
要求y=log ![]() cos(
cos( ![]() ﹣2x)的递增区间是,即求t=﹣sin2x的减区间,
﹣2x)的递增区间是,即求t=﹣sin2x的减区间,
即求y=sin2x的增区间,
由2kπ﹣ ![]() ≤2x<2kπ,k∈Z,得kπ﹣
≤2x<2kπ,k∈Z,得kπ﹣ ![]() ≤x<kπ,k∈Z,
≤x<kπ,k∈Z,
即y=sin2x的增区间是[﹣ ![]() +kπ,kπ)(k∈Z),
+kπ,kπ)(k∈Z),
故选:B
【考点精析】本题主要考查了函数的单调性和复合函数单调性的判断方法的相关知识点,需要掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种;复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”才能正确解答此题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2= ![]() ,anbn+1+bn+1=nbn . (Ⅰ)求{an}的通项公式;
,anbn+1+bn+1=nbn . (Ⅰ)求{an}的通项公式;
(Ⅱ)求{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AC=2 ![]() ,AA1=
,AA1= ![]() ,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
(Ⅱ)求二面角B﹣A1D﹣C的大小.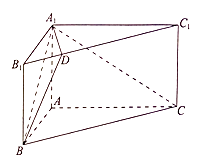
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知圆C的圆心是x﹣y+1=0与x轴的交点,且与直线x+y+3=0相切,求圆C的标准方程;
(2)若点P(x,y)在圆x2+y2﹣4y+3=0上,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且右准线方程为x=5.
,且右准线方程为x=5.
(1)求椭圆方程;
(2)过椭圆右焦点F作斜率为1的直线l与椭圆C交于A,B两点,P为椭圆上一动点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ ![]() )+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
)+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( ) 
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com