
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 图像在
图像在![]() 处的切线方程;
处的切线方程;
(2)证明:![]() ;
;
(3)若不等式![]() 对于任意的
对于任意的![]() 均成立,求实数
均成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)利用导数的几何意义求曲线在点![]() 处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率
处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率![]() ;(2)利用导数方法证明不等式
;(2)利用导数方法证明不等式![]() 在区间
在区间![]() 上恒成立的基本方法是构造函数
上恒成立的基本方法是构造函数![]() ,然后根据函数的单调性,或者函数的最值证明函数
,然后根据函数的单调性,或者函数的最值证明函数![]() ,其中一个重要的技巧就是找到函数
,其中一个重要的技巧就是找到函数![]() 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式;(3)对于恒成立的问题,常用到两个结论:(1)
在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式;(3)对于恒成立的问题,常用到两个结论:(1)![]() 恒成立
恒成立![]() ,(2)
,(2)![]() 恒成立
恒成立![]() .
.
试题解析:(1)![]()
![]() ,
,![]()
![]() 又由
又由![]() ,
,
得切线![]() ,即
,即![]()
(2)设![]() ,则
,则![]() ,令
,令![]() 得
得![]()
|
| 1 |
|
|
| 极大值 |
|
|
| 0 |
|
![]()
![]() ,即
,即![]() .
.
(3)![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,![]() 不满足不等式;
不满足不等式;
当![]() 时,设
时,设![]() ,
,![]() ,令
,令![]() ,得
,得![]()
|
|
|
|
|
| 极大值 |
|
|
| 0 |
|
![]()
![]()
综上![]()


科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,点K(-1,0)为直线l与抛物线C准线的交点,直线l与抛物线C相交于A,B两点.
(1)求抛物线C的方程;
(2)设![]() ·
·![]() =
=![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某学校高一年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成6组:第1组
之间,将测量结果按如下方式分成6组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
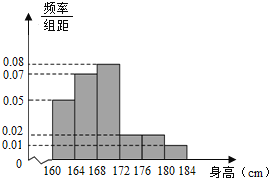
(1)求这50名男生身高的中位数,并估计该校高一全体男生的平均身高;
(2)求这50名男生当中身高不低于176![]() 的人数,并且在这50名身高不低于176
的人数,并且在这50名身高不低于176![]() 的男生中任意抽取2人,求这2人身高都低于180
的男生中任意抽取2人,求这2人身高都低于180![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:(1)终边相同的角的同名三角比的值相等;(2)终边不同的角的同名三角比的值不同;(3)若![]() ,则
,则![]() 是第一或第二象限角;(4)△
是第一或第二象限角;(4)△![]() 中,若
中,若![]() ,则
,则![]() ;其中正确命题的个数是( )
;其中正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入12月以来,某地区为了防止出现重污染天气,坚持保民生、保蓝天,严格落实机动车限行等一系列“管控令”.该地区交通管理部门为了了解市民对“单双号限行”的赞同情况,随机采访了220名市民,将他们的意见和是否拥有私家车情况进行了统计,得到如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“是否赞同限行与是否拥有私家车”有关;
(2)为了了解限行之后是否对交通拥堵、环境污染起到改善作用,从上述调查的不赞同限行的人员中按分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少抽到1名“没有私家车”人员的概率.
附:![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经济开发区规划要修建一地下停车场,停车场横截面是如图所示半椭圆形AMB,其中AP为2百米,BP为4百米,![]() ,M为半椭圆上异于A,B的一动点,且
,M为半椭圆上异于A,B的一动点,且![]() 面积最大值为
面积最大值为![]() 平方百米,如图建系.
平方百米,如图建系.
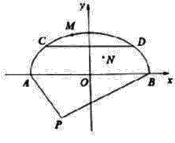
![]() 求出半椭圆弧的方程;
求出半椭圆弧的方程;
![]() 若要将修建地下停车场挖出的土运到指定位置P处,N为运土点,以A,B为出口,要使运土最省工,工程部需要指定一条分界线,请求出分界线所在的曲线方程;
若要将修建地下停车场挖出的土运到指定位置P处,N为运土点,以A,B为出口,要使运土最省工,工程部需要指定一条分界线,请求出分界线所在的曲线方程;
![]() 若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设
若在半椭圆形停车场的上方修建矩形商场,矩形的一边CD与AB平行,设![]() 百米,试确定t的值,使商场地面的面积最大.
百米,试确定t的值,使商场地面的面积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com