
【题目】设函数  ,若对任意的x∈R,f(x)>x恒成立,则实数a的取值范围是( )
,若对任意的x∈R,f(x)>x恒成立,则实数a的取值范围是( )
A.(﹣2,e)
B.(﹣∞,e)
C.(1,+∞)
D.(﹣∞,1)
【答案】A
【解析】解:设 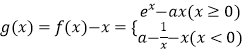 ,
,
依题意可知g(x)>0恒成立,
⑴当x<0时, ![]() ,
,
∴a>﹣2;
⑵当x≥0时,f′(x)=ex﹣a,当a∈(﹣2,1]时,f′(x)≥0,f(x)单调递增,
所以f(x)min=f(0)=1>0,满足题意;
当a>1时,令f′(x)=0,得x=lna,
当x∈[0,lna)时,f′(x)<0,f(x)单调递减,
当x∈(lna,+∞)时,f′(x)>0,f(x)单调递增,
所以当x=lna时,f(x)取得极小值,且为最小值f(lna)=a﹣alna,
根据题意,a﹣alna>0,所以1﹣lna>0,lna<1,a<e,
∴a∈(1,e).
综上所述,实数a的取值范围是(﹣2,e).
故答案为:A.
由题意可得设 g ( x ) = f ( x ) x,对分段函数进行讨论,当x<0时, g ( x )=a+(![]() )+(x),根据基本不等式可得 g ( x )≥ a + 2 > 0, 即得a>﹣2。当x≥0时,求导可得f′(x)≥0,f(x)单调递增,即得f(x)min=f(0)=1>0。利用导数求得函数增减性和最小值,根据题意,a﹣alna>0解得1<a<e,综上所述实数a的取值范围是(﹣2,e)。
)+(x),根据基本不等式可得 g ( x )≥ a + 2 > 0, 即得a>﹣2。当x≥0时,求导可得f′(x)≥0,f(x)单调递增,即得f(x)min=f(0)=1>0。利用导数求得函数增减性和最小值,根据题意,a﹣alna>0解得1<a<e,综上所述实数a的取值范围是(﹣2,e)。


科目:高中数学 来源: 题型:
【题目】某同学为研究函数 ![]() 的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的值域是 .
的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的值域是 . 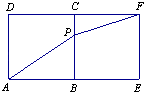
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex﹣2x﹣2a,且a∈[1,2],设函数f(x)在区间[0,ln2]上的最小值为m,则m的取值范围是( )
A.[﹣2,﹣2ln2]
B.[﹣2,﹣ ![]() ]
]
C.[﹣2ln2,﹣1]
D.[﹣1,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ=a(a>0),Q为l上一点,以OQ为边作等边三角形OPQ,且O、P、Q三点按逆时针方向排列.
(Ⅰ)当点Q在l上运动时,求点P运动轨迹的直角坐标方程;
(Ⅱ)若曲线C:x2+y2=a2 , 经过伸缩变换 ![]() 得到曲线C′,试判断点P的轨迹与曲线C′是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
得到曲线C′,试判断点P的轨迹与曲线C′是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002,…,800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;(下面摘取了第7行到第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100人的数学与地理的水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的人数共有20+18+4=42.
①若在该样本中,数学成绩优秀率是30%,求a,b的值;
②在地理成绩及格的学生中,已知a≥11,b≥7,求数学成绩优秀人数比及格人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣kx+k(k∈R).
(Ⅰ)求f(x)在[1,2]上的最小值;
(Ⅱ)若 ![]() ,对x∈(﹣1,1)恒成立,求正数a的最大值.
,对x∈(﹣1,1)恒成立,求正数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|ax﹣1|,若实数a>0,不等式f(x)≤3的解集是{x|﹣1≤x≤2}.
(Ⅰ)求a的值;
(Ⅱ)若 ![]() <|k|存在实数解,求实数k的取值范围.
<|k|存在实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四支足球队进行单循环比赛(每两队比赛一场),每场比赛胜者得3分,负者得0分,平局双方各得1分.比赛结束后发现没有足球队全胜,且四队得分各不相同,则所有比赛中最多可能出现的平局场数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com