
【题目】在区间[0,2]上任取两个实数a,b,则函数f(x)=x3+ax﹣b在区间[﹣1,1]上有且只有一个零点的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:由题意知本题是一个几何概型, ∵a∈[0,2],
∴f'(x)=3x2+a≥0,
∴f(x)是增函数
若f(x)在[﹣1,1]有且仅有一个零点,
则f(﹣1)f(1)≤0
∴(﹣1﹣a﹣b)(1+a﹣b)≤0,
即(1+a+b)(1+a﹣b)≥0 ![]() =
= ![]() 11
11
由线性规划内容知全部事件的面积为2×2=4,满足条件的面积4﹣ ![]() =
= ![]()
∴P= ![]() =
= ![]()
故选D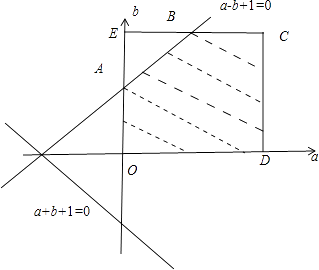
【考点精析】掌握几何概型和函数的零点是解答本题的根本,需要知道几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣kx+k.
(Ⅰ)若f(x)≥0有唯一解,求实数k的值;
(Ⅱ)证明:当a≤1时,x(f(x)+kx﹣k)<ex﹣ax2﹣1.
(附:ln2≈0.69,ln3≈1.10, ![]() ,e2≈7.39)
,e2≈7.39)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0). (Ⅰ)求证:f(x)≥8恒成立;
|+|x﹣2m|(m>0). (Ⅰ)求证:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参与舒城中学数学选修课的同学对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图.
定价x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

参考数据:
![]() ,
,
![]() .
.
(1)根据散点图判断y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)当定价为150元/千克时,试估计年销量.
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估计分别为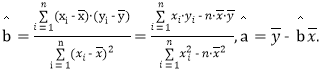
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国建“精准扶贫,产业扶贫”的战略,某市面向全国征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示 
(1)求图中x的值
(2)在抽出的100名志愿者中按年龄采取分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人,记这3名志愿者中“年龄低于35岁”的人数为Y,求Y的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ea(x﹣1)﹣ax2 , a为不等于零的常数.
(Ⅰ)当a<0时,求函数f′(x)的零点个数;
(Ⅱ)若对任意x1 , x2 , 当x1<x2时,f(x2)﹣f(x1)>a( ![]() ﹣2x1)(x2﹣x1)恒成立,求实数a的取值范围.
﹣2x1)(x2﹣x1)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】整改校园内一块长为15 m,宽为11 m的长方形草地(如图A),将长减少1 m,宽增加1 m(如图B).问草地面积是增加了还是减少了?假设长减少x m,宽增加x m(x>0),试研究以下问题:

x取什么值时,草地面积减少?
x取什么值时,草地面积增加?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com