
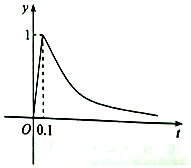
 ���������彡��������ɱ�֣�������������������ij����ʵ��������������������������ҿ���������ʵ�鷢�֣����ڽ����ͷ������Ĺ����У������������ĺ���Ũ��y��mg/m3����ʱ��t��h�������ȣ��ͷ���Ϻ�y��t�ĺ�����ϵΪy=��$\frac{1}{16}$��t-a��aΪ����������ͼ����֪�����ҵĿ����к���Ũ����0.25mg/m3����ʱ���������ʺ�����������ͼ����Ϣ����һ���ͷ�������ʼ����������0.575h���ʺ�������
���������彡��������ɱ�֣�������������������ij����ʵ��������������������������ҿ���������ʵ�鷢�֣����ڽ����ͷ������Ĺ����У������������ĺ���Ũ��y��mg/m3����ʱ��t��h�������ȣ��ͷ���Ϻ�y��t�ĺ�����ϵΪy=��$\frac{1}{16}$��t-a��aΪ����������ͼ����֪�����ҵĿ����к���Ũ����0.25mg/m3����ʱ���������ʺ�����������ͼ����Ϣ����һ���ͷ�������ʼ����������0.575h���ʺ������� ���� �ȹ۲�ͼ��0��t��0.1ʱ��ֱ�ߣ���t��0.1ʱ��ͼ�����0.1��1�����ݴ˷ֱ�д�������ϵĺ�������ʽ��������÷ֶκ�������ʽд����ҩ��y�����ˣ���ʱ��t��Сʱ��֮��ĺ�����ϵʽ���ɣ���y��0.25���뼴���������ʱ�䣮
��� �⣺�۲�ͼ��0��t��0.1ʱ��ֱ�ߣ�
��y=10t��
��t��0.1ʱ��ͼ�����0.1��1����
��y=��$\frac{1}{16}$��t-0.1��
�ຬҩ��y�����ˣ���ʱ��t��Сʱ��֮��ĺ�����ϵʽΪ��
y=$\left\{\begin{array}{l}{10t��0��t��0.1}\\{��\frac{1}{16}��^{t-0.1}��t��0.1}\end{array}\right.$��
��10t��0.25��0��t��0.1���ɵ�0.025��t��0.1��
�ɣ�$\frac{1}{16}$��t-0.1��$\frac{1}{4}$��
���t��0.6��
��t��0.1���ɵ�0.1��t��0.6��
��0.1-0.025+0.6-0.1=0.575��
��������0.575Сʱ���ʺ������˶���
�ʴ�Ϊ��0.575h��
���� ���⿼���˷ֶκ������Լ������뷽�̵�˼�룬���ν�ϵ�˼�뷽�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��-2b����a2��4b2 | B�� | ��a2��4b2����a��-2b | ||
| C�� | ��a��-2b����a2��4b2 | D�� | ��a2=4b2����a=-2b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{40\sqrt{10}}{3}$�� | B�� | $\frac{64\sqrt{2}}{3}$�� | C�� | $\frac{8\sqrt{2}}{3}$�� | D�� | 8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�$\frac{1}{2}$�� | B�� | ��-�ޣ�0] | C�� | ��0��+�ޣ� | D�� | ��-�ޣ�0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{\sqrt{2}}{2}$��4�� | B�� | ��0��$\frac{1}{4}$�� | C�� | ��$\frac{1}{4}$��$\frac{\sqrt{2}}{2}$�� | D�� | ��$\frac{1}{4}$��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��4} | B�� | {0��1��4} | C�� | {0��2} | D�� | {0��1��2��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B�� | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | C�� | $\frac{x^2}{4}-{y^2}=1$ | D�� | ${x^2}-\frac{y^2}{4}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$akm | B�� | 2akm | C�� | $\sqrt{5}$akm | D�� | $\sqrt{7}$akm |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com