
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,A1C1⊥B1D1 , E,F分别是AB,BC的中点. 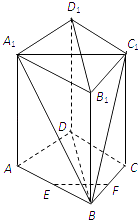
(1)求证:EF∥平面A1BC1;
(2)求证:平面D1DBB1⊥平面A1BC1 .
【答案】
(1)解:连接AC,则AC∥A1C1,而E,F分别是AB,BC的中点,
∴EF∥AC,
则EF∥A1C1,故EF∥平面A1BC1
(2)解:因为BB1⊥平面A1B1C1D1,所以BB1⊥A1C1,又A1C1⊥B1D1,
则A1C1⊥平面D1DBB1
又A1C1平面A1BC1,所以平面D1DBB1⊥平面A1BC1
【解析】(1)连接AC,则AC∥A1C1 , E,F分别是AB,BC的中点,可得EF∥AC,然后再利用直线与平面平行的判定定理进行证明,即可解决问题;(2)因为BB1⊥平面A1B1C1D1 , 所以BB1⊥A1C1 , 又A1C1⊥B1D1 , 然后利用平面与平面垂直的判定定理进行证明;
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为R的偶函数f(x)满足对于任意实数x,都有f(1+x)=f(1﹣x),且当0≤x≤1时,f(x)=3x+1 .
(1)求证:函数f(x)是周期函数;
(2)当x∈[1,3]时,求f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为公差不为0的等差数列{an}的前n项和,且a1=1,S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关系式中正确的是( )
A.sin 11°<cos 10°<sin 168°
B.sin 168°<sin 11°<cos 10°
C.sin 11°<sin 168°<cos 10°
D.sin 168°<cos 10°<sin 11°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,b(sinωx,0),且ω>0,设函数f(x)=(a+b)b+k.
,b(sinωx,0),且ω>0,设函数f(x)=(a+b)b+k.
(1)若f(x)的图像中相邻两条对称轴间的距离不小于 ![]() ,求ω的取值范围.
,求ω的取值范围.
(2)若f(x)的最小正周期为π,且当 ![]() 时,f(x)的最大值是2,求k的值.
时,f(x)的最大值是2,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心M在x轴上,半径为1,直线 ![]() ,被圆M所截的弦长为
,被圆M所截的弦长为 ![]() ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.
(I)求圆M的方程;
(II)设A(0,t),B(0,t+6)(﹣5≤t≤﹣2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a3=3,S11=0.
(1)求数列{an}的通项公式;
(2)当n为何值时,Sn最大,并求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的正三角形中, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 上的点,且满足
上的点,且满足![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() .(如图2)
.(如图2)
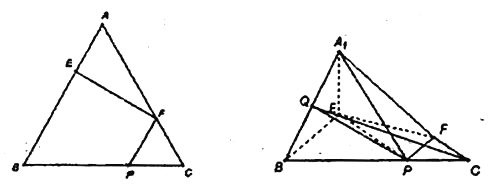
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)求![]() 与平面
与平面![]() 所成角的正切.
所成角的正切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com