【题目】在正四面体ABCD中，M，N分别是BC和DA的中点，则异面直线MN和CD所成角为 ．
【答案】
【解析】解：如图，取AC中点O，连结AM、DM、OM、ON，
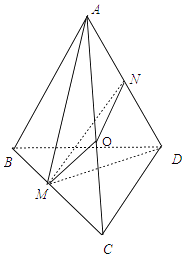
设正四面体ABCD的棱长为2，
∵M，N分别是BC和DA的中点，
∴AM=DM= 
，MN= 
，
MN 
=1，NO 
=1，
∴∠MNO是异面直线MN和CD所成角（或所成角的补角），
cos∠MNO= 
= 
= 
，
∴∠MNO= ．
∴异面直线MN和CD所成角为 ．
所以答案是： ．
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．
科目：高中数学 来源： 题型：
【题目】(2015·江苏）已知集合X={1，2，3}，Yn={1,2,3...,n}(n
N*)，Sn={(a,b)|a整除b或b整除a， aX, bYn}, 令f(n)表示集合Sn所包含元素的个数。
（1）写出f（6）的值；
（2）当n≥6时，写出f(n)的表达式，并用数学归纳法证明.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】F1、F2为椭圆的两个焦点，以F2为圆心作圆F2 ， 已知圆F2经过椭圆的中心，且与椭圆相交于M点，若直线MF1恰与圆F2相切，则该椭圆的离心率e为（ ）
A.
﹣1
B.2﹣
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】假设关于某设备的使用年限x和支出的维修费用y（万元），有如下表的统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系，试求：
（1）线性回归方程 
.
（2）估计使用年限为10年时，维修费用是多少.
（3）计算总偏差平方和、残差平方和及回归平方和.
（4）求 
并说明模型的拟合效果.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了研究某高校大学5000名新生的视力情况，随机地抽查了该校100名进校新生的视力情况，得到其频率分布直方图如右图，若规定视力低于5.0的学生属[于近视学生，则估计该校新生中不是近视的人数约为（ ）
A.300人
B.400人
C.600人
D.1000人
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}中，a1= 
，an+1= 
（n∈N*）．
（Ⅰ）求证：数列{ 
}是等差数列，并求{an}的通项公式；
（Ⅱ）设bn+an=l（n∈N*），Sn=b1b2+b2b3+…+bnbn+1 ， 试比较an与8Sn的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知边长为1的正方形 
与 
所在的平面互相垂直，点 
分别是线段 
上的动点（包括端点）， 
，设线段 
的中点的轨迹为 
，则 的长度为（ ）
A.
B.
C.
D.2
查看答案和解析>>
科目：高中数学 来源： 题型：
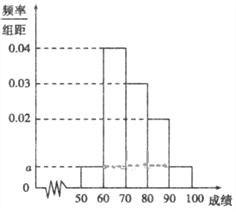
【题目】某校
名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:
,
,
,
,
.
(1).求图中
的值; 并根据频率分布直方图,估计这100名学生语文成绩的平均分;
(2).若这100名学生语文成绩某些分数段的人数(
)与数学成绩相应分数段的人数(
)之比如上右表所示,求数学成绩在
之外的人数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C的方程：
和直线l的方程：
，点P是圆C上动点，直线l与两坐标轴交于A、B两点．
(1)求与圆C相切且垂直于直线l的直线方程；
(2)求
面积的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com