
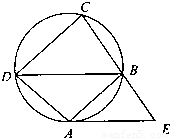
 如图,在圆内接梯形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=5,BE=4,则弦BD的长为 .
如图,在圆内接梯形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=5,BE=4,则弦BD的长为 . 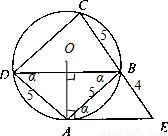 解:如图连结圆心O与A,因为过点A作圆的切线与CB的延长线交于点E.所以OA⊥AE,
解:如图连结圆心O与A,因为过点A作圆的切线与CB的延长线交于点E.所以OA⊥AE, =6,
=6, ,AB=AD=5,
,AB=AD=5, .
.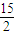 .
.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
 ,在圆内接梯形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=5,BE=4,则弦BD的长为
,在圆内接梯形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=5,BE=4,则弦BD的长为| 15 |
| 2 |
| 15 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013年普通高等学校招生全国统一考试天津卷文数 题型:022
如图,在圆内接梯形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=5,BE=4,则弦BD的长为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图, 在圆内接梯形ABCD中, AB//DC, 过点A作圆的切线与CB的延长线交于点E. 若AB = AD = 5, BE = 4, 则弦BD的长为 . 
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练12练习卷(解析版) 题型:填空题
如图,在圆内接梯形ABCD中,AB∥DC.过点A作圆的切线与CB的延长线交于点E.若AB=AD=5,BE=4,则弦BD的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com