
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,以
中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置(
的位置(![]() 平面
平面![]() ).
).

(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2020年疫情的到来给我们生活学习等各方面带来种种困难.为了顺利迎接高考,省里制定了周密的毕业年级复学计划.为了确保安全开学,全省组织毕业年级学生进行核酸检测的筛查.学生先到医务室进行咽拭子检验,检验呈阳性者需到防疫部门做进一步检测.已知随机抽一人检验呈阳性的概率为0.2%,且每个人检验是否呈阳性相互独立,若该疾病患病率为0.1%,且患病者检验呈阳性的概率为99%.若某人检验呈阳性,则他确实患病的概率( )
A.0.99%B.99%C.49.5%.D.36.5%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知纵坐标不同的两点![]() ,
,![]() 为椭圆
为椭圆![]() 上的两个点,且
上的两个点,且![]() ,
,![]() ,
,![]() 三点共线,线段
三点共线,线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,则直线
轴的正半轴,建立平面直角坐标系,则直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求圆![]() 的直角坐标方程,并求出圆心坐标和半径;
的直角坐标方程,并求出圆心坐标和半径;
(2)求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.

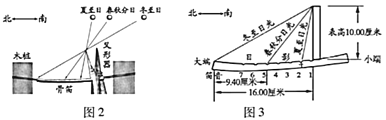
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角坐标系![]() 中,曲线
中,曲线![]() 由中心在原点,焦点在
由中心在原点,焦点在![]() 轴上的半椭圆和以原点为圆心,半径为2的半圆构成,以坐标原点
轴上的半椭圆和以原点为圆心,半径为2的半圆构成,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.

(1)写出曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com