
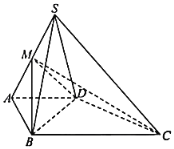
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 都是等边三角形,且点
都是等边三角形,且点![]() 在底面
在底面![]() 上的射影为
上的射影为![]() .
.

(1)证明:![]() 为
为![]() 的中点;
的中点;
(2)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接AC,取AC的中点N,连接MN,DN,利用线面垂直的判定证明点M在底面上的射影为N,结合点M在底而ABCD上的射影为O,可得N与O重合,即O为AC的中点;
(2)设![]() ,
,![]() ,求解三角形可得
,求解三角形可得![]() .再由DA=DC,O是AC的中点,得
.再由DA=DC,O是AC的中点,得![]() ,得到
,得到![]() ,故异面直线MD与BC所成角为
,故异面直线MD与BC所成角为![]() .在
.在![]() 中求解
中求解![]() ,可得异面直线
,可得异面直线![]() 与
与![]() 所成的角.
所成的角.
(1)证明:接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
∵![]() 与
与![]() 都是等边三角形且公共边为
都是等边三角形且公共边为![]() ,
,
∴![]() ,
,
又∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() ,故点
,故点![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,
,
又已知点![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,
,
∴![]() 与
与![]() 重合即
重合即![]() 为
为![]() 的中点;
的中点;

(2)设![]() ,
,![]() ,
,
∵![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
则![]() ,
,![]() ,
,
![]() ,
,
![]()
则![]() ,
,
∴![]() ,
,
故![]() ,
,
又∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
故异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
即异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的长轴长为
的长轴长为![]() ,点
,点![]() 、
、![]() 、
、![]() 为椭圆上的三个点,
为椭圆上的三个点,![]() 为椭圆的右端点,
为椭圆的右端点,![]() 过中心
过中心![]() ,且
,且![]() ,
,![]() .
.

(1)求椭圆的标准方程;
(2)设![]() 、
、![]() 是椭圆上位于直线
是椭圆上位于直线![]() 同侧的两个动点(异于
同侧的两个动点(异于![]() 、
、![]() ),且满足
),且满足![]() ,试讨论直线
,试讨论直线![]() 与直线
与直线![]() 斜率之间的关系,并求证直线
斜率之间的关系,并求证直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是椭圆
是椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为椭圆上异于
为椭圆上异于![]() 、
、![]() 的一点.
的一点.
(1)![]() 是椭圆
是椭圆![]() 的上顶点,且直线
的上顶点,且直线![]() 与直线
与直线![]() 垂直,求点
垂直,求点![]() 到
到![]() 轴的距离;
轴的距离;
(2)过点![]() 的直线
的直线![]() (不过坐标原点)与椭圆
(不过坐标原点)与椭圆![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 在
在![]() 轴上方,点
轴上方,点![]() 在
在![]() 轴下方,若
轴下方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他门各应偿还多少?该问题中,1斗为10升,则羊主人应偿还多少升粟?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,左右焦点分别为![]() ,
,![]() 的椭圆的离心率为
的椭圆的离心率为![]() ,焦距为
,焦距为![]() ,A,B是椭圆上两点.
,A,B是椭圆上两点.
(1)若直线![]() 与以原点为圆心的圆相切,且
与以原点为圆心的圆相切,且![]() ,求此圆的方程;
,求此圆的方程;
(2)动点P满足:![]() ,直线
,直线![]() 与
与![]() 的斜率的乘积为
的斜率的乘积为![]() ,求动点P的轨迹方程.
,求动点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,![]() ,点M是SA的中点,
,点M是SA的中点,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 平面SCD;
平面SCD;
(2)若直线SD与底面ABCD所成的角为![]() ,求平面MBD与平面SBC所成的锐二面角的余弦值.
,求平面MBD与平面SBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成![]() 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
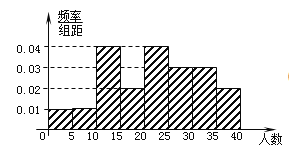
A.  B.
B. 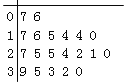
C. 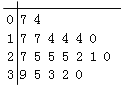 D.
D. 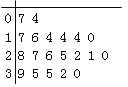
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com