
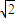 y+z=1,则|OP|的最小值等于 .
y+z=1,则|OP|的最小值等于 . 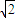 y+z=1内的射影重合时,|OP|取得最小值.再求经过原点与平面x+
y+z=1内的射影重合时,|OP|取得最小值.再求经过原点与平面x+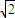 y+z=1垂直的直线与平面x+
y+z=1垂直的直线与平面x+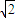 y+z=1的交点Q,利用距离公式求出OQ的长,即可得到|OP|取得最小值.
y+z=1的交点Q,利用距离公式求出OQ的长,即可得到|OP|取得最小值.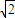 y+z=1内的点,
y+z=1内的点,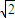 y+z=1内的射影重合时,|OP|取得最小值
y+z=1内的射影重合时,|OP|取得最小值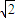 y+z=1垂直的直线方向向量为
y+z=1垂直的直线方向向量为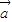 =(1,
=(1, ,1)
,1)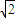 y+z=1垂直的直线方程为:
y+z=1垂直的直线方程为: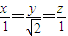
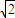 y+z=1内的射影点为Q(
y+z=1内的射影点为Q( ,
,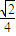 ,
, )
)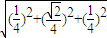 =
=




 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com