练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知A、B、C、D是空间不共面的四个点，且AB⊥CD，AD⊥BC，则直线BD与AC（ ）
    A．垂直
    B．平行
    C．相交
    D．位置关系不确定
    【答案】分析：过点A做AO⊥面BCD，垂足为O，由条件结合三垂线定理得O为△BCD的垂心，所以DO⊥BC，从而AD⊥BC．
    解答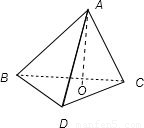：解：过点A做AO⊥面BCD，垂足为O，
    因为AB⊥CD，由三垂线定理可知BO⊥CD，
    同理：DO⊥BC，
    所以O为△BCD的垂心，
    所以CO⊥BD，
    所以BD⊥AC．
    故选A
    点评：本题考查两条直线位置关系的判定、三垂线定理和逆定理的应用，考查空间想象能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    12、已知A、B、C、D是空间不共面的四个点，且AB⊥CD，AD⊥BC，则直线BD与AC（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A，B，C，D是抛物线y2=4x上四点，F是焦点，且
    FA
    +
    FB
    +
    FC
    =
    0
    ，则|
    FA
    |+|
    FB
    |+|
    FC
    |    =（　　）
    A、4B、6C、8D、10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•北京模拟）已知a、b、c、d是公比为2的等比数列，则
    2a+b
    2c+d
    =（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A、B、C、D是球面上四点，若AB=AC=
    		2
    ，BD=DC=CB=2，二面角A-BC-D的平面角等于150°，则该球的表面积为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•甘肃三模）已知A，B，C，D是同一球面上的四个点，其中△ABC是正三角形，AD⊥平面ABC，AD=2AB=6，则该球的表面积为（　　）

    查看答案和解析>>

    同步练习册答案