
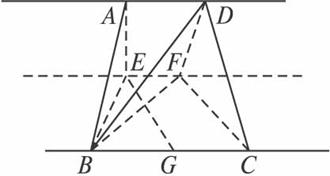
(1)当θ=90°且AE=2时,证明BD⊥EG.
(2)(理)若θ=60°,BE=EF=![]() ,求二面角DBFC的大小.
,求二面角DBFC的大小.
(文)设AE=x,若sinθ=1![]() (0<x<4),求棱锥F—BCD的体积V(x)的最大值.
(0<x<4),求棱锥F—BCD的体积V(x)的最大值.
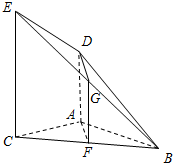
答案:证明:(1)过点D作DH⊥EF,垂足为H.连结HB、GH.∵AD∥EH∥BG,且截面ABE⊥EF,∴AD=EH=BG=BE=2.∴四边形BGHE为菱形.又BE⊥EH,∴四边形BGHE为正方形.
∴EG⊥HB.又DH⊥EF,且θ=90°,∴DH⊥面BCFE.由三垂线定理得BD⊥EG.
(2)(理)∵截面AEB⊥EF,∴∠AEB即为二面角AEFC的平面角,即∠AEB=60°.∵BE=EF=![]() ,∴AE=
,∴AE=![]() .∴由余弦定理得AB2=
.∴由余弦定理得AB2=![]() .显然AE2=BE2+AB2,∴△ABE为直角三角形,即AB⊥BE.又AB⊥EF,∴AB⊥面BCFE.连结DG,则DG∥AB,∴DG⊥面CBEF.
.显然AE2=BE2+AB2,∴△ABE为直角三角形,即AB⊥BE.又AB⊥EF,∴AB⊥面BCFE.连结DG,则DG∥AB,∴DG⊥面CBEF.
作GM⊥BF,垂足为M,连结DM,则∠DMG为二面角DBFC的平面角.
∵BE=EF=![]() ,∴BF=
,∴BF=![]() .∵S△BGF=
.∵S△BGF=![]() BG·BE=
BG·BE=![]() BF·MG,∴GM=
BF·MG,∴GM=![]() .∴在△DGM中,tan∠DMG=
.∴在△DGM中,tan∠DMG=![]() ,即所求的二面角的大小为arctan
,即所求的二面角的大小为arctan![]() .
.
(注:也可用空间向量求解,步骤略)
(文)∵截面AEB⊥EF,∴∠AEB即为二面角AEFC的平面角,即∠AEB=θ.又∵AD∥面BFC,
∴V(x)=VA—BFC=![]() S△BFC·AEsinθ=
S△BFC·AEsinθ=![]() ·
·![]() ·4·(4-x)·x(1-
·4·(4-x)·x(1-![]() )=
)=![]() x(4-x)2.
x(4-x)2.
∴令V′(x)=![]() (3x2-16x+16)=0,得x=
(3x2-16x+16)=0,得x=![]() .∵0<x<
.∵0<x<![]() 时,V′(x)>0,
时,V′(x)>0,![]() <x<4时,V′(x)<0,
<x<4时,V′(x)<0,
∴x=![]() 时,V(x)有最大值,其值为
时,V(x)有最大值,其值为![]() .
.


科目:高中数学 来源: 题型:
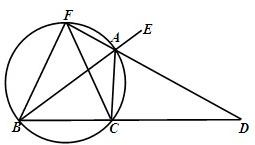 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.查看答案和解析>>
科目:高中数学 来源: 题型:
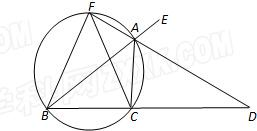 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.查看答案和解析>>
科目:高中数学 来源: 题型:
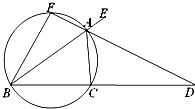 (2013•怀化三模)如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,∠BFA=90°,∠EAC=120°,BC=6cm,则AD的长=
(2013•怀化三模)如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,∠BFA=90°,∠EAC=120°,BC=6cm,则AD的长=| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•东城区一模)如图,已知AD⊥平面ABC,CE⊥平面ABC,F为BC的中点,若AB=AC=AD=
(2013•东城区一模)如图,已知AD⊥平面ABC,CE⊥平面ABC,F为BC的中点,若AB=AC=AD=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com