
【题目】2018年高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试,现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
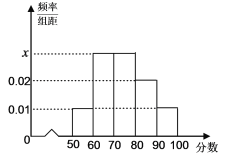
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(Ⅰ)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
(Ⅱ)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取2人参加这次考试的考后分析会,试求![]() 组中至少有1人被抽到的概率.
组中至少有1人被抽到的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(Ⅰ)先计算第2、3组的频率和,再根据概率求x的值,再利用中位数公式求所抽取的50名学生成绩的中位数.( Ⅱ)利用古典概型求![]() 组中至少有1人被抽到的概率.
组中至少有1人被抽到的概率.
详解:(Ⅰ)由频率分布直方图可得第2、3组的频率和为
![]() , 故
, 故![]() .
.
设中位数为![]() 分,则有
分,则有![]() ,
,![]() ,
,
即所求的中位数为![]() 分.
分.
(Ⅱ)由(Ⅰ)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.
记成绩在![]() 这组的3名学生分别为
这组的3名学生分别为![]() ,
,![]() ,
,![]() ,成绩在
,成绩在![]() 这组的2名学生分别为
这组的2名学生分别为![]() ,
,![]() ,成绩在
,成绩在![]() 这组的1名学生为
这组的1名学生为![]() ,则从中任抽取3人的所有可能结果为
,则从中任抽取3人的所有可能结果为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .共15种.
.共15种.
其中![]() 组中至少有1人被抽到的所有可能结果为
组中至少有1人被抽到的所有可能结果为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .共12种
.共12种
故![]() 组中至少有1人被抽到的概率
组中至少有1人被抽到的概率![]() .
.


 能力评价系列答案
能力评价系列答案科目:高中数学 来源: 题型:
【题目】共享汽车的出现为我们的出行带来了极大的便利,当然也为投资商带来了丰厚的利润。现某公司瞄准这一市场,准备投放共享汽车。该公司取得了在![]() 个省份投放共享汽车的经营权,计划前期一次性投入
个省份投放共享汽车的经营权,计划前期一次性投入![]() 元. 设在每个省投放共享汽车的市的数量相同(假设每个省的市的数量足够多),每个市都投放
元. 设在每个省投放共享汽车的市的数量相同(假设每个省的市的数量足够多),每个市都投放![]() 辆共享汽车.由于各个市的多种因素的差异,在第
辆共享汽车.由于各个市的多种因素的差异,在第![]() 个市的每辆共享汽车的管理成本为(
个市的每辆共享汽车的管理成本为(![]() )元(其中
)元(其中![]() 为常数).经测算,若每个省在
为常数).经测算,若每个省在![]() 个市投放共享汽车,则该公司每辆共享汽车的平均综合管理费用为
个市投放共享汽车,则该公司每辆共享汽车的平均综合管理费用为![]() 元.(本题中不考虑共享汽车本身的费用)
元.(本题中不考虑共享汽车本身的费用)
注:综合管理费用=前期一次性投入的费用+所有共享汽车的管理费用,平均综合管理费用=综合管理费用÷共享汽车总数.
(1)求![]() 的值;
的值;
(2)问要使该公司每辆共享汽车的平均综合管理费用最低,则每个省有几个市投放共享汽车?此时每辆共享汽车的平均综合管理费用为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在边长为12的正方形AA'A1'A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1'分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A'A1'与AA1重合,构成如图2所示的三棱柱ABC﹣A1B1C1.

(1)求三棱锥P﹣ABC与三棱锥Q﹣PAC的体积之和;
(2)求直线AQ与平面BCC1B1所成角的正弦值;
(3)求三棱锥Q﹣ABC的外接球半径r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台风中心在港口南偏东![]() 方向上,距离港口
方向上,距离港口![]() 千米处的海面上形成,并以每小时
千米处的海面上形成,并以每小时![]() 千米的速度向正北方向移动,距台风中心
千米的速度向正北方向移动,距台风中心![]() 千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )
千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比在B地晚![]()
秒. A地测得该仪器弹至最高点H时的仰角为30°.
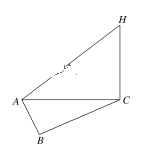
(1)求A、C两地的距离;
(2)求该仪器的垂直弹射高度CH.(声音的传播速度为340米/秒)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com