
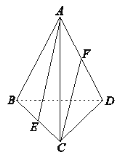
【题目】如图,在三棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正三角形,
的正三角形,![]() ,且
,且![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点,则异面直线
中点,则异面直线![]() 与
与![]() 所成角的余弦值为__________.
所成角的余弦值为__________.
科目:高中数学 来源: 题型:
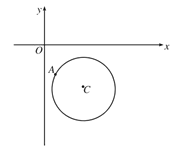
【题目】如图,在平面直角坐标系![]() 中,已知以C为圆心的圆
中,已知以C为圆心的圆![]() 及其上一点
及其上一点![]() .
.
(1)设平行于![]() 的直线
的直线![]() 与圆C相交于
与圆C相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设点![]() 满足:存在圆C上的两点
满足:存在圆C上的两点![]() 使得
使得![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的定义域分别为
的定义域分别为![]() ,若存在常数
,若存在常数![]() ,满足:①对任意
,满足:①对任意![]() ,恒有
,恒有![]() ,且
,且![]() .②对任意
.②对任意![]() ,关于
,关于![]() 的不等式组
的不等式组![]()
![]() 恒有解,则称
恒有解,则称![]() 为
为![]() 的一个“
的一个“![]() 型函数”.
型函数”.
(1)设函数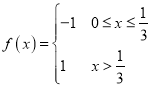 和
和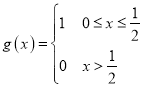 ,求证:
,求证:![]() 为
为![]() 的一个“
的一个“![]() 型函数”;
型函数”;
(2)设常数![]() ,函数
,函数![]() ,
,![]() .若
.若![]() 为
为![]() 的一个“
的一个“![]() 型函数”,求
型函数”,求![]() 的取值范围;
的取值范围;
(3)设函数![]() .问:是否存在常数
.问:是否存在常数![]() ,使得函数
,使得函数![]() 为
为![]() 的一个“
的一个“![]() 型函数”?若存在,求
型函数”?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名学生作为样本测量身高.测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组![]() ;第二组
;第二组![]() ;…;第八组
;…;第八组![]() .下图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组与第八组人数之和为第七组的两倍.
.下图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组与第八组人数之和为第七组的两倍.
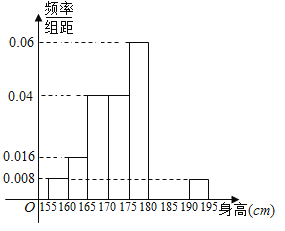
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)求第六组和第七组的频率并补充完整频率分布直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,其中
,其中![]() ,
,![]() 是非空数集且
是非空数集且![]() .设
.设![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)是否存在实数![]() ,使得
,使得![]() ,且
,且![]() ?若存在,求出所有满足条件的
?若存在,求出所有满足条件的![]() ;若不存在,说明理由;
;若不存在,说明理由;
(3)若![]() 且
且![]() ,
,![]() ,
,![]() 单调递增,求集合
单调递增,求集合![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com