
【题目】某水产品经销商销售某种鲜鱼,售价为每千克![]() 元,成本为每千克
元,成本为每千克![]() 元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失
元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失![]() 元.根据以往的市场调查,将市场日需求量(单位:千克)按
元.根据以往的市场调查,将市场日需求量(单位:千克)按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到如图的频率分布直方图.
进行分组,得到如图的频率分布直方图.

(Ⅰ)未来连续三天内,连续两天该种鲜钱的日需求量不低于![]() 千克,而另一天的日需求量低于
千克,而另一天的日需求量低于![]() 千克的概率;
千克的概率;
(Ⅱ)在频率分布直方图的日需求量分组中,以各组区间的中点值代表该组的各个值,并以日需求量落入该区间的频率作为日需求量取该区间中点值的概率.若经销商每日进货![]() 千克,记经销商每日利润为
千克,记经销商每日利润为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(Ⅰ)0.192(Ⅱ)见解析
【解析】
(Ⅰ)根据频率分布直方图,即可求出连续两天该种鲜鱼的日销售量不低于350公斤,而另一天日销售量低于350公斤的概率,
(Ⅱ)结合频率分布直方图求得利润的可能取值,列出分布列,求出数学期望.
(Ⅰ)由频率分布直方图可知,
日需求量不低于![]() 千克的概率为
千克的概率为![]() ,
,
则未来连续三天内,有连续两天的日需求量不低于![]() 千克,而另一天日需求量低于
千克,而另一天日需求量低于![]() 千克的概率为
千克的概率为
![]()
![]() .
.
(Ⅱ)日需求量的可能取值为100,200,300,400,500,
当日需求量为100时,利润为(20-15)![]() 100-300
100-300![]() =-400,
=-400,
当日需求量为200时,利润为(20-15)![]() 200-200
200-200![]() =400,
=400,
当日需求量为300时,利润为(20-15)![]() 300-100
300-100![]() =1200,
=1200,
当日需求量为400或500时,利润为(20-15)![]() 400=2000,
400=2000,
所以![]() 可取的值是
可取的值是![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
![]() ;
;
![]()
![]()
所以![]() 的分布列:
的分布列:
|
|
|
|
|
|
|
|
|
|
此时利润的期望值![]()
![]() (元).
(元).


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题:①任意两条直线都可以确定一个平面;②若两个平面有3个不同的公共点,则这两个平面重合;③直线a,b,c,若a与b共面,b与c共面,则a与c共面;④若直线l上有一点在平面α外,则l在平面α外.其中错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地因受天气,春季禁渔等因素影响,政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为![]() 的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
捕鱼量(单位:吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表(捕鱼期内的每个晴好天气渔船方可捕鱼,非晴好天气不捕鱼):
晴好天气(单位:天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
(同组数据以这组数据的中间值作代表)
(Ⅰ)估计渔业捕捞队吨位为![]() 的渔船单次出海的捕鱼量的平均数
的渔船单次出海的捕鱼量的平均数![]() ;
;
(Ⅱ)已知当地鱼价为2万元/吨,此种捕鱼船在捕鱼期内捕鱼时,每天成本为10万元/艘,若不捕鱼,每天成本为2万元/艘,若以(Ⅰ)中确定的![]() 作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①请依据往年天气统计数据,试估计一艘此种捕鱼船年利润不少于1600万元的概率;
②设今后3年中,此种捕鱼船每年捕鱼情况一样,记一艘此种捕鱼船年利润不少于1600万元的年数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
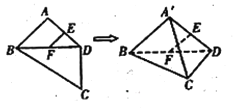
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数 ,回归直线方程
,回归直线方程![]() ,
,
其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惠州市某学校需要从甲、乙两名学生中选1人参加数学竞赛,抽取了近期两人5次数学考试的分数,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲 | 80 | 85 | 71 | 92 | 87 |
乙 | 90 | 76 | 75 | 92 | 82 |
(1)若从甲、乙两人中选出1人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中答题方案如下:
每人从5道备选题中随机抽取3道作答,若至少答对其中2道,则可参加复赛,否则被淘汰.假设被选中参赛的学生只会5道备选题中的3道,求该学生能进人复赛的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下5条表述中,横线上填A代表“充分非必要条件”,填B代表“必要非充分条件”,填C代表“充要条件”,填D代表“既非充分也非必要条件”,请将相应的字母填入下列横线上.
(1)若![]() ,则“
,则“![]() 是
是![]() 与
与![]() 的等比中项”是“
的等比中项”是“![]() ”的_______.
”的_______.
(2)“数列![]() 为常数列”是“数列
为常数列”是“数列![]() 既是等差数列又是等比数列”的_______.
既是等差数列又是等比数列”的_______.
(3)若![]() 是等比数列,则“
是等比数列,则“![]() ”是“
”是“![]() 为递减数列”的_______.
为递减数列”的_______.
(4)若![]() 是公比为
是公比为![]() 的等比数列,则“
的等比数列,则“![]() ”是“
”是“![]() 是递减数列”的_______.
是递减数列”的_______.
(5)记数列![]() 的前
的前![]() 项和为
项和为![]() ,则“数列
,则“数列![]() 为递增数列”是“数列
为递增数列”是“数列![]() 的各项均为大于零”的_______.
的各项均为大于零”的_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com