
分析 (1)利用点$P({\frac{a}{2},\;\frac{{\sqrt{2}a}}{2}})$在椭圆上,推出2a2=3b2,结合b2=a2-c2,求解椭圆C的离心率.
(2)设直线l的方程为y=k(x+c)+c=kx+(k+1)c,推出椭圆C的方程为$\frac{x^2}{{3{c^2}}}+\frac{y^2}{{2{c^2}}}=1$,判断点A在椭圆C内,设直线l与椭圆C的交点为M(x1,y1),N(x2,y2),联立方程组,通过韦达定理求解k即可.
解答 解:(1)∵点$P({\frac{a}{2},\;\frac{{\sqrt{2}a}}{2}})$在椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$上
∴$\frac{a^2}{{4{a^2}}}+\frac{{2{a^2}}}{{4{b^2}}}=1$,
∴2a2=3b2…(1分)
∵b2=a2-c2
∴2a2=3a2-3c2
∴a2=3c2…(3分)
∴椭圆C的离心率$e=\frac{c}{a}=\frac{{\sqrt{3}}}{3}$…(5分)
(2)显然,直线l的斜率存在,设为k,则直线l的方程为y=k(x+c)+c=kx+(k+1)c
…(6分)
由(1)知b2=3c2-c2=2c2,∴椭圆C的方程为$\frac{x^2}{{3{c^2}}}+\frac{y^2}{{2{c^2}}}=1$
即2x2+3y2=6c2,显然点A在椭圆C内…(7分)
设直线l与椭圆C的交点为M(x1,y1),N(x2,y2),
椭圆C的方程与直线l的方程联立消去y得(3k2+2)x2+6k(k+1)cx+3(k+1)2c2-6c2=0…(8分)
∴${x_1}+{x_2}=\frac{{-6k({k+1})c}}{{3{k^2}+2}}$…(10分)
∵$\frac{{{x_1}+{x_2}}}{2}=-c$,∴$-2c=\frac{{-6k({k+1})c}}{{3{k^2}+2}}$∴3k(k+1)=3k2+2
∴$k=\frac{2}{3}$…(12分)
点评 本题考查直线与椭圆额综合应用,椭圆的简单性质的应用,考查分析问题解决问题的能力.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+4 | B. | f(x)=log2x | C. | f(x)=2x | D. | $f(x)=3+\frac{2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y-1)2=4 | B. | x2+(y-$\frac{1}{2}$)2=1 | C. | (x-1)2+y2=4 | D. | (x-$\frac{1}{2}$)2+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
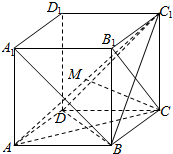 如图,在棱长为1的正方体ABCD-A1B1C1D1中,给出以下结论:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,给出以下结论:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
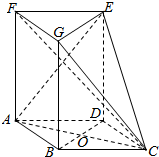 如图,在多面体ABCD-EFG中,O是菱形ABCD的对角线AC与BD的交点,四边形ABGF,ADEF都是矩形.
如图,在多面体ABCD-EFG中,O是菱形ABCD的对角线AC与BD的交点,四边形ABGF,ADEF都是矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com