
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
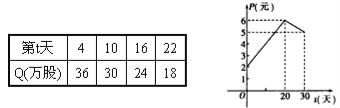
(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
【答案】(1) 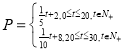 (2)
(2) ![]() (3) 在30天中的第15天,日交易额的最大值为125万元
(3) 在30天中的第15天,日交易额的最大值为125万元
【解析】
试题分析:(1)根据图象可知此函数为分段函数,在(0,20]和(20,30]两个区间利用待定系数法分别求出一次函数关系式联立可得P的解析式;(2)因为Q与t成一次函数关系,根据表格中的数据,取出两组即可确定出Q的解析式;(3)根据股票日交易额=交易量×每股较易价格可知y=PQ,可得y的解析式,分别在各段上利用二次函数求最值的方法求出即可
试题解析:(1)由图像知,前20天满足的是递增的直线方程,且过两点(0,2),(20,6),容易求得![]() ;从20天到30天满足递减的直线方程,且过两点(20,6),(30,5),求得方程为
;从20天到30天满足递减的直线方程,且过两点(20,6),(30,5),求得方程为![]() ,
,
故P(元)与时间t(天)所满足的函数关系式为:
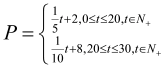 。。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。。4分
(2)由图表,易知Q与t满足一次函数关系,
即![]() . ................7分
. ................7分
(3)由(1)(2)可知

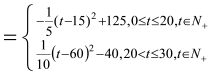 .........................9分
.........................9分
当![]() ,t=15时,
,t=15时,![]() . .......................10分
. .......................10分
当![]() 时,y随t的增大而减小. .........................11分
时,y随t的增大而减小. .........................11分
所以,在30天中的第15天,日交易额的最大值为125万元. .......12分


科目:高中数学 来源: 题型:
【题目】设命题p:x>0,x-lnx>0,则¬p为
A. x0>0,x0-lnx0>0 B. x0>0,x0-lnx0≤0
C. x>0,x-lnx<0 D. x>0,x-lnx≤0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-![]() .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,第二步归纳假设应写成( )
A.假设n=2k+1(k∈N*)正确,再推n=2k+3正确
B.假设n=2k﹣1(k∈N*)正确,再推n=2k+1正确
C.假设n=k(k∈N*)正确,再推n=k+1正确
D.假设n=k(k≥1)正确,再推n=k+2正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化城市环境,某市针对市民乱扔垃圾现象进行罚款处理。为了更好的了解市民的态度,随机抽取了200人进行了调查,得到如下数据:
罚款金额 | 0 | 5 | 10 | 15 | 20 |
会继续乱扔垃圾的人数 | 80 | 50 | 40 | 20 | 10 |
(1)若乱扔垃圾的人数![]() 与罚款金额
与罚款金额![]() 满足线性回归方程,求回归方程
满足线性回归方程,求回归方程![]() ,其中
,其中![]() ,并据此分析,要使乱扔垃圾者不超过
,并据此分析,要使乱扔垃圾者不超过 ,罚款金额至少是多少元?
,罚款金额至少是多少元?
(2)若以调查数据为基础,从5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆心坐标为(![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y=![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=![]() x分别相切于C、D两点.
x分别相切于C、D两点.
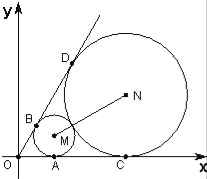
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com