
【题目】已知函数![]() ,那么下列结论中错误的是( )
,那么下列结论中错误的是( )
A. 若![]() 是
是![]() 的极小值点,则
的极小值点,则![]() 在区间
在区间![]() 上单调递减
上单调递减
B. ![]() ,使
,使![]()
C. 函数![]() 的图像可以是中心对称图形
的图像可以是中心对称图形
D. 若![]() 是
是![]() 的极值点,则
的极值点,则![]()
【答案】A
【解析】分析:对于选项A,先求导得![]() ,设其对应方程
,设其对应方程![]() 的两根为
的两根为![]() 。根据一元二次不等式的解法可得函数
。根据一元二次不等式的解法可得函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,由此可得选项A说法错误;由选项A的解题过程可得选项B、D正确;对于选项C,取特殊值
,由此可得选项A说法错误;由选项A的解题过程可得选项B、D正确;对于选项C,取特殊值![]() ,得特殊函数
,得特殊函数![]() ,因为函数
,因为函数![]() 为奇函数,所以选项C正确。
为奇函数,所以选项C正确。
详解:对于选项A,![]() ,假设方程
,假设方程![]() 的两根为
的两根为![]() 。根据一元二次不等式的解法可得:由
。根据一元二次不等式的解法可得:由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ,所以函数
,所以函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,极小值点为
,极小值点为![]() ,所以选项A错误;
,所以选项A错误;
对于选项B,由选项A的解题过程可知在区间![]() 上,一定
上,一定![]() ,使
,使![]() ,所以选项B正确。
,所以选项B正确。
对于选项C,当![]() 时,函数
时,函数![]() ,此函数图像关于原点对称。所以选项C正确;
,此函数图像关于原点对称。所以选项C正确;
对于选项D,由选项A的解题过程可知:若![]() 是
是![]() 的极值点,则
的极值点,则![]() 。所以选项D正确。
。所以选项D正确。
故选A。


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为![]() ,
,![]() ,
,![]() ,乙协会编号为
,乙协会编号为![]() ,丙协会编号分别为
,丙协会编号分别为![]() ,
,![]() ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP. 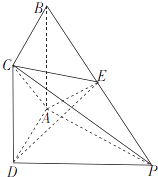
(1)证明:AC⊥DE;
(2)若PC= ![]() BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部分在该市随机调查了![]() 户居民六月份的用电量(单位:
户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:
![]() .
.
对应的家庭收入数据如下:
![]()
![]() .
.
(Ⅰ)根据国家发改委的指示精神,该市计划实施![]() 阶阶梯电价,使
阶阶梯电价,使![]() 的用户在第一档,电价为
的用户在第一档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第二档,电价为
的用户在第二档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第三档,电价为
的用户在第三档,电价为![]() 元/
元/![]() ,试求出居民用电费用
,试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系;
间的函数关系;
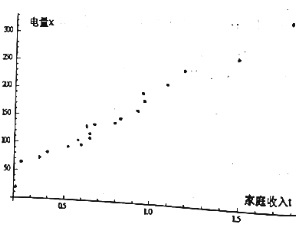
(Ⅱ)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数).
的回归直线方程(回归直线方程的系数四舍五入保留整数).
(Ⅲ)小明家的月收入![]() 元,按上述关系,估计小明家月支出电费多少元?
元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() ,
,![]() ,…,
,…,![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为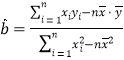 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 与
与![]() 有表格中的数据,且
有表格中的数据,且![]() 与
与![]() 线性相关,由最小二乘法得
线性相关,由最小二乘法得![]() .
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求![]() 与
与![]() 的线性回归方程;
的线性回归方程;
(2)现有第二个线性模型:![]() ,且
,且![]() .若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
.若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中:
①若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
③若![]() ,满足
,满足![]() ,则
,则![]() 的最小值为
的最小值为![]()
④函数![]() 的最小值为
的最小值为![]()
正确的有__________.(把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3﹣x2=2.(12分)
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系xOy中,依次连接点P1(x1 , 1),P2(x2 , 2)…Pn+1(xn+1 , n+1)得到折线P1 P2…Pn+1 , 求由该折线与直线y=0,x=x1 , x=xn+1所围成的区域的面积Tn . 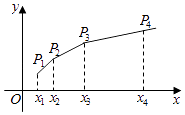
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,
,![]() .
.
(1)直线![]() 是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
(2)已知点![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 满足条件
满足条件![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com