
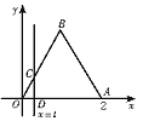
| ∵△ABC是正三角形,且边长为2,
∴图中各点坐标为A(2,0),B(1, ∵|DA|=2-t,同法yC= ∴当0≤t≤1时,y=f(t)= 当1<t≤2时,y=f(t)=S△OAB-S△CDA= - 再注意到,当t<0时,显然有y=0,当t>2时,有y= ∴y=f(t)= 此函数的定义域为R,值域为[0,
|


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:013
如图△
OAB是边长为2的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(见图阴影部分)为y,则函数y=f(t)的大致图形为下图中的[
]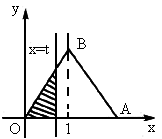
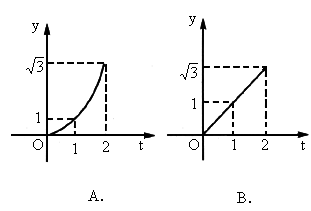
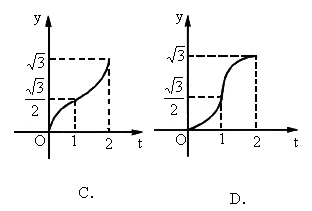
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
如图△OAB是边长为2的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(见图阴影部分)为y,则函数y=f(t)的大致图形为下图中的
[ ]
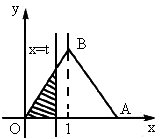
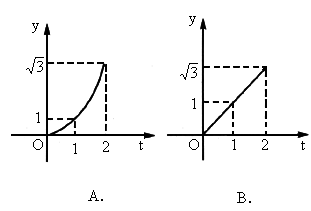
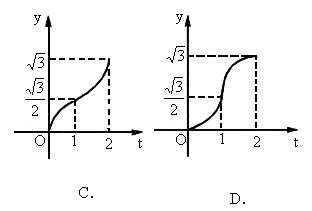
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com