
分析 (1)求出f′(x)=$\frac{1-lnx}{x2}$(x>0),通过判断函数的单调性,求解函数的最大值即可.
(2)求出g′(x)=lnx-ax=x($\frac{lnx}{x}$-a),由(1)及x∈(0,e]:通过①当a=$\frac{1}{e}$时,②当a∈[0,$\frac{1}{e}$),分别求解函数的单调性与最值即可.
解答 解:(1)f′(x)=$\frac{1-lnx}{x2}$(x>0),
当x∈(0,e)时,f′(x)>0,f(x)单调递增;
当x∈(e,+∞)时,f′(x)<0,f(x)单调递减,
所以当x=e时,f(x)取得最大值f(e)=$\frac{1}{e}$.…(4分)
(2)g′(x)=lnx-ax=x($\frac{lnx}{x}$-a),由(1)及x∈(0,e]得:
①当a=$\frac{1}{e}$时,$\frac{lnx}{x}$-a≤0,g′(x)≤0,g(x)单调递减,
当x=e时,g(x)取得最小值g(e)=h(a)=-$\frac{e}{2}$.…(6分)
②当a∈[0,$\frac{1}{e}$),f(1)=0≤a,f(e)=$\frac{1}{e}$>a,
所以存在t∈[1,e),g′(t)=0且lnt=at,
当x∈(0,t)时,g′(x)<0,g(x)单调递减,
当x∈(t,e]时,g′(x)>0,g(x)单调递增,
所以g(x)的最小值为g(t)=h(a).…(9分)
令h(a)=G(t)=$\frac{tlnt}{2}$-t,
因为G′(t)=$\frac{lnt-1}{2}$<0,所以G(t)在[1,e)单调递减,此时G(t)∈(-$\frac{e}{2}$,-1].
综上,h(a)∈[-$\frac{e}{2}$,-1].…(12分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,CA=CB=AA1,∠BAA1=∠BAC=60°,点O是线段AB的中点.
如图,在三棱柱ABC-A1B1C1中,CA=CB=AA1,∠BAA1=∠BAC=60°,点O是线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积为S为( )(注:圆台侧面积公式为S=π(R+r)l)
如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积为S为( )(注:圆台侧面积公式为S=π(R+r)l)| A. | 17π+3$\sqrt{17}$π | B. | 20π+5$\sqrt{17}$π | C. | 22π | D. | 17π+5$\sqrt{17}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
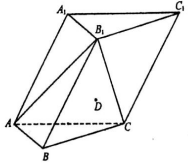 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值为0 | D. | f(x)与0的大小关系不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com