
【题目】己知一个动点M在圆![]() 上移动,它与定点
上移动,它与定点![]() 所连线段的中点为P.
所连线段的中点为P.
(1)求点P的轨迹方程.
(2)过定点![]() 的直线与点P的轨迹交于A,B两点,求弦AB的中点C的轨迹.
的直线与点P的轨迹交于A,B两点,求弦AB的中点C的轨迹.
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x+1.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程:
(2)若非零实数a使得f(x)![]() ax
ax![]() ax2
ax2![]() 对x∈[1,+∞)恒成立,求a的取值范围.
对x∈[1,+∞)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,智能手机的更新换代极其频繁和快速,而青少年对新事物的追求更是强烈,为了调查大学生更换手机的时间,现对某大学中的大学生使用一部手机的年限进行了问卷调查,并从参与调查的大学生中抽取了男生、女生各![]() 人进行抽样分析,制成如下的频率分布直方图.
人进行抽样分析,制成如下的频率分布直方图.

(1)根据频率分布直方图,估计男大学生使用手机年限的中位数和女大学生使用手机年限的众数;
(2)根据频率分布直方图,求出男大学生和女大学生使用手机年限的平均值,并分析比较男大学生和女大学生哪个群体更换手机的频率更高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .过原点
.过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(1)求椭圆![]() 长半轴长;
长半轴长;
(2)求![]() 最大值;
最大值;
(3)若直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 的面积与
的面积与![]() 的面积的乘积为定值.
的面积的乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
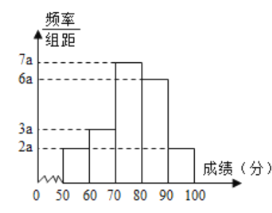
(1)求频率分布直方图中![]() 的值;
的值;
(2)估计总体中成绩落在![]() 中的学生人数;
中的学生人数;
(3)根据频率分布直方图估计![]() 名学生数学考试成绩的众数,中位数.
名学生数学考试成绩的众数,中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,A,B两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 | A组统计结果 | B组统计结果 | ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.求这60人中“年龄达到35岁且偶尔使用单车”的人数;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我边防局接到情报,在海礁![]() 所在直线
所在直线![]() 的一侧点
的一侧点![]() 处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕:如图,已知快艇出发位置在
处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕:如图,已知快艇出发位置在![]() 的另一侧码头
的另一侧码头![]() 处,
处,![]() 公里,
公里,![]() 公里,
公里,![]() ;
;

(1)是否存在点![]() ,使快艇沿航线
,使快艇沿航线![]() 或
或![]() 的路程相等;如存在,则建立适当的直角坐标系,求出点
的路程相等;如存在,则建立适当的直角坐标系,求出点![]() 的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由;
的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由;
(2)问走私船在怎样的区域上时,路线![]() 比路线
比路线![]() 的路程短,请说明理由.
的路程短,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
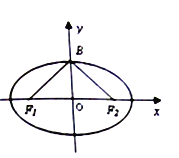
【题目】如图,已知椭圆![]() 的焦点和上项点分别为
的焦点和上项点分别为![]() ,我们称
,我们称![]() 为椭圆
为椭圆![]() 的“特征三角形”.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 若椭圆
的“特征三角形”.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 若椭圆![]() ,直线
,直线![]()
![]() 已知椭圆
已知椭圆![]() 与椭圆
与椭圆![]() 是相似椭圆,求
是相似椭圆,求![]() 的值及椭圆
的值及椭圆![]() 与椭圆
与椭圆![]() 相似比;
相似比;
![]() 求点
求点![]() 到椭圆
到椭圆![]() 上点的最大距离;
上点的最大距离;
![]() 如图,设直线
如图,设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() 两点,求证:
两点,求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com