
【题目】(导学号:05856333)
已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其右焦点为F(c,0),第一象限的点A在椭圆C上,且AF⊥x轴.
,其右焦点为F(c,0),第一象限的点A在椭圆C上,且AF⊥x轴.
(Ⅰ)若椭圆C过点(1,- ![]() ),求椭圆C的标准方程;
),求椭圆C的标准方程;
(Ⅱ)已知直线l:y=x-c与椭圆C交于M,N两点,且B(4c,yB)为直线l上的点,证明:直线AM,AB,AN的斜率满足kAB=![]() .
.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)运用椭圆的离心率公式和点满足椭圆方程,结合a,b,c的关系,解方程可得a,b,进而得到椭圆方程;
(2)由离心率公式可得椭圆C的方程为3x2+4y2=12c2,将直线方程代入椭圆方程,运用韦达定理,再由直线的斜率公式化简整理,即可得证.
试题解析:
(Ⅰ)依题意, 解得a=2,b=
解得a=2,b=![]() ,c=1,
,c=1,
故椭圆C的标准方程为![]() +
+![]() =1.
=1.
(Ⅱ)因为e=,故a=2c,b=![]() c,
c,
∴椭圆C:3x2+4y2=12c2,
将直线l的方程为y=x-c代入椭圆方程并整理,得7x2-8cx-8c2=0,
设M(x1,y1),N(x2,y2),则有x1+x2=![]() ,x1·x2=-
,x1·x2=-![]() ,可知B的坐标为(4c,3c),
,可知B的坐标为(4c,3c),
A的坐标为(c, c),故kAM+kAN=![]() +
+![]() =
=![]() ,
,
将x1+x2=![]() ,x1·x2=-
,x1·x2=-![]() 代入可得,kAM+kAN=1,kAB=
代入可得,kAM+kAN=1,kAB=![]() =,
=,
∴kAB=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文、理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.

(1)求a的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,并判断能否有超过95%的把握认为“获奖与学生的文、理科有关”?
文科生 | 理科生 | 合计 | |
获奖 | 5 | ||
不获奖 | |||
合计 | 200 |
附表及公式: 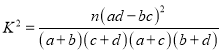
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
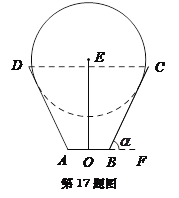
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856310)
已知函数f(x)=x+![]() +ln x(a∈R).
+ln x(a∈R).
(Ⅰ)当a=2时, 求函数f(x)的单调区间;
(Ⅱ)若关于x的函数g(x)=![]() -f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
-f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856323)已知在△ABC中,A,B,C所对的边分别为a,b,c,R为△ABC外接圆的半径,若a=1, ![]() sin2B+
sin2B+![]() sin2C-sin2A=sin Asin Bsin C,则R的值为( )
sin2C-sin2A=sin Asin Bsin C,则R的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在![]() 三组对应的人数依次成等差数列
三组对应的人数依次成等差数列

(1)求频率分布直方图中![]() 的值.
的值.
(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com