
【题目】已知函数![]() 有三个不同的零点
有三个不同的零点![]() ,
, ![]() ,
, ![]() (其中
(其中![]() ),则
),则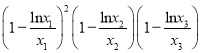 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】令f(x)=0,分离变量可得a=![]() ,
,
令g(x)=![]() ,
,
由g′(x)=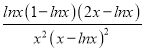 =0,得x=1或x=e.
=0,得x=1或x=e.
当x∈(0,1)时,g′(x)<0;当x∈(1,e)时,g′(x)>0;当x∈(e,+∞)时,g′(x)<0.
即g(x)在(0,1),(e,+∞)上为减函数,在(1,e)上为增函数.
∴0<x1<1<x2<e<x3,
a=![]() =
=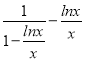 ,令μ=
,令μ=![]() ,
,
则a=![]() ﹣μ,即μ2+(a﹣1)μ+1﹣a=0,
﹣μ,即μ2+(a﹣1)μ+1﹣a=0,
μ1+μ2=1﹣a<0,μ1μ2=1﹣a<0,
对于μ=![]() ,μ′=
,μ′=![]()
则当0<x<e时,μ′>0;当x>e时,μ′<0.而当x>e时,μ恒大于0.
画其简图,
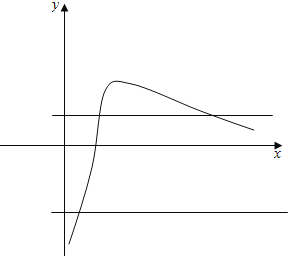
不妨设μ1<μ2,则μ1=![]() ,μ2=
,μ2=![]() =
=![]() =μ3,
=μ3,
∴(1﹣![]() )2(1﹣
)2(1﹣![]() )(1﹣
)(1﹣![]() )=(1﹣μ1)2(1﹣μ2)(1﹣μ3)
)=(1﹣μ1)2(1﹣μ2)(1﹣μ3)
=[(1﹣μ1)(1﹣μ2)]2=[1﹣(1﹣a)+(1﹣a)]2=1.
故选:D.


科目:高中数学 来源: 题型:
【题目】![]() 两城相距
两城相距![]() ,在两城之间距
,在两城之间距![]() 城
城![]() 处建一核电站给
处建一核电站给![]() 两城供电,为保证城市安全,核电站距城市距离不得小于
两城供电,为保证城市安全,核电站距城市距离不得小于![]() .已知供电费用等于供电距离
.已知供电费用等于供电距离![]() 的平方与供电量(亿度)之积的
的平方与供电量(亿度)之积的![]() 倍,若
倍,若![]() 城供电量为每月20亿度,城供电量为每月10亿度.
城供电量为每月20亿度,城供电量为每月10亿度.
(1)把月供电总费用![]() 表示成
表示成![]() 的函数;
的函数;
(2)核电站建在距![]() 城多远,才能使供电总费用
城多远,才能使供电总费用![]() 最少?
最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12![]() 海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;在A处看灯塔C在货轮的北偏西30°,距离为8![]() 海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 函数f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的图象关于原点对称,其中m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[﹣2,2]上是单调函数;
(3)当﹣2≤x≤2 时,不等式f(x)≥(n﹣logma)logma恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?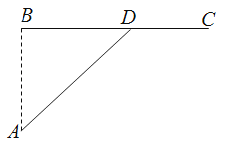
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轴截面是边长为4 ![]() 的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为
的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为 ![]() ,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( ) 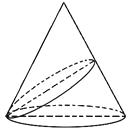
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),且对任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),则实数a的取值范围是( )
A.[3,+∞)
B.(0,3]
C.[ ![]() ,3]
,3]
D.(0, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别是a,b,c,已知2cosA(bcosC+ccosB)=a.
(1)求角A;
(2)若a= ![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com