
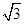 ,那么当该棱锥的体积最大时,它的高为( )
,那么当该棱锥的体积最大时,它的高为( )| A.1 | B.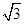 | C.2 | D.3 |
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
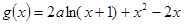 .
.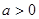 时,讨论函数
时,讨论函数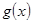 的单调性;
的单调性;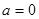 时,在函数
时,在函数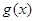 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为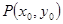 ,试探究函数
,试探究函数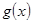 在Q
在Q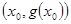 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?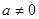 时
时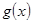 图象是否存在不同的两点A、B具有(2)问中所得出的结论.
图象是否存在不同的两点A、B具有(2)问中所得出的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的导函数为
的导函数为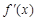 ,那么下列说法正确的是( )
,那么下列说法正确的是( )A.若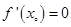 ,则 ,则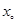 是函数 是函数 的极值点 的极值点 |
B.若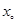 是函数 是函数 的极值点,则 的极值点,则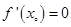 |
C.若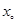 是函数 是函数 的极值点,则 的极值点,则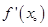 可能不存在 可能不存在 |
D.若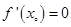 无实根 ,则函数 无实根 ,则函数 必无极值点 必无极值点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com