
【题目】已知椭圆![]() 的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,若点
,若点![]() 总在以线段
总在以线段![]() 为直径的圆内,求
为直径的圆内,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)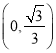
【解析】试题分析:(I)由题意列出方程组求出![]() ,
, ![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程.(Ⅱ)当直线
的方程.(Ⅱ)当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() 的方程为
的方程为![]() ,
, ![]() ,点B在椭圆内,由
,点B在椭圆内,由 ,得
,得![]() ,由此利用根的判别式、韦达定理、弦长公式、由此能求出
,由此利用根的判别式、韦达定理、弦长公式、由此能求出![]() 的取值范围.
的取值范围.
试题解析:(I)解:由题意,得:  又因为
又因为![]()
解得![]() ,所以椭圆C的方程为
,所以椭圆C的方程为![]() .
.
(II)当直线![]() 的斜率不存在时,由题意知
的斜率不存在时,由题意知![]() 的方程为x=0,
的方程为x=0,
此时E,F为椭圆的上下顶点,且![]() ,
,
因为点![]() 总在以线段
总在以线段![]() 为直径的圆内,且
为直径的圆内,且![]() ,
,
所以![]() ,故点B在椭圆内.
,故点B在椭圆内.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() .
.
由方程组 得
得![]() ,
,
因为点B在椭圆内,
所以直线![]() 与椭圆C有两个公共点,即
与椭圆C有两个公共点,即![]() .
.
设![]() ,则
,则![]() .
.
设EF的中点![]() ,则
,则![]() ,
,
所以![]() .所以
.所以 ,
,
![]() ,
,
因为点D总在以线段EF为直径的圆内,所以![]() 对于
对于![]() 恒成立.
恒成立.
所以![]() .
.
化简,得![]() ,整理,得
,整理,得![]() ,
,
而![]() (当且仅当k=0时等号成立)所以
(当且仅当k=0时等号成立)所以![]() ,
,
由m>0,得![]() .综上,m的取值范围是
.综上,m的取值范围是![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】某企业根据供销合同生产某种型号零件10万件,规定:零件长度(单位:毫米)在区间![]() 内,则为一等品;若长度在
内,则为一等品;若长度在![]() 或
或![]() 内,则为二等品;否则为不合格产品.现从生产出的零件中随机抽取100件作样本,其长度数据的频率分布直方图如图所示.
内,则为二等品;否则为不合格产品.现从生产出的零件中随机抽取100件作样本,其长度数据的频率分布直方图如图所示.
(1)试估计该样本的平均数;
(2)根据合同,企业生产的每件一等品可获利10元,每件二等品可获利8元,每件不合格产品亏损6元,若用样本估计总体,试估算该企业生产这批零件所获得的利润.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Sn为数列{an}的前n项和,已知an>0,an2+2an=4Sn+3
(I)求{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若![]() <t<
<t<![]() ,求证:方程f(x)=0在区间(-1,0)及
,求证:方程f(x)=0在区间(-1,0)及![]() 内各有一个实数根.
内各有一个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人——宰相宰相西萨班达依尔.国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每一小格都比前一小格加一倍.请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!”国王觉得这要求太容易满足了,就命令给他这些麦粒.当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求.那么,宰相要求得到的麦粒到底有多少粒?下面是四位同学为了计算上面这个问题而设计的程序框图,其中正确的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=﹣1,c=1,d=0.1,则输出的x的值为( )
A.﹣0.6
B.﹣0.69
C.﹣0.7
D.﹣0.71
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC﹣A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1 . 
(1)求证:平面A1BC⊥平面ABC1;
(2)若直线AA1与底面ABC所成的角为60°,求直线AA1与平面ABC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项的和,且Sn =![]() (an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.
(an -1)(n∈N*), 数列{bn }的通项公式bn = 4n+5.
①求证:数列{an }是等比数列;
②若d∈{a1 ,a2 ,a3 ,……}∩{b1 ,b2 ,b3 ,……},则称d为数列{an }和{bn }的公共项,按它们在原数列中的先后顺序排成一个新的数列{dn },求数列{dn }的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com