
【题目】设常数a使方程sinx+ ![]() cosx=a在闭区间[0,2π]上恰有三个解x1 , x2 , x3 , 则x1+x2+x3= .
cosx=a在闭区间[0,2π]上恰有三个解x1 , x2 , x3 , 则x1+x2+x3= .
科目:高中数学 来源: 题型:
【题目】某二手车交易市场对某型号的二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程:(参考公式:
的回归直线方程:(参考公式: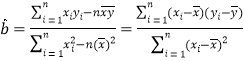 ,
, ![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中混装着9个大小相同的球(编号不同),其中5只白球,4只红球,为了把红球与白球区分开来,采取逐只抽取检查,若恰好经过5次抽取检查,正好把所有白球和红球区分出来了,则这样的抽取方式共有__________种(用数字作答) .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥A﹣BCD及其侧视图、俯视图如图所示,设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP. 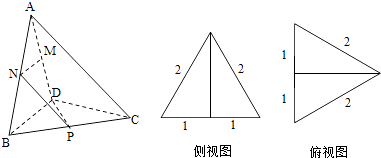
(1)证明:P是线段BC的中点;
(2)求二面角A﹣NP﹣M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次![]() 函数,分别从集合
函数,分别从集合![]() 和
和![]() 中随机取一个数
中随机取一个数![]() 和
和![]() 得到数对
得到数对![]() .
.
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 有零点的概率;
有零点的概率;
(2)若![]() ,
, ![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数.
(1)全体排成一行,其中男生必须排在一起;
(2)全体排成一行,男、女各不相邻;
(3)全体排成一行,其中甲不在最左边,乙不在最右边;
(4)全体排成一行,其中甲、乙、丙三人从左至右的顺序不变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)过椭圆![]() 的右顶点
的右顶点![]() 做相互垂直的两条直线
做相互垂直的两条直线![]() ,
,![]() ,分别交椭圆
,分别交椭圆![]() 于
于![]() 、
、![]() (
(![]() 、
、![]() 异于点
异于点![]() ),问直线
),问直线![]() 是否通过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
是否通过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com