
【题目】已知等差数列{an}满足a2=3,a3+a5=2
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn及Sn的最大值.
【答案】
(1)解:设数列{an}公差为d,
∵等差数列{an}满足a2=3,a3+a5=2,
∴ 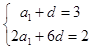 ,
,
解得a1=4,d=﹣1,
∴an=a1+(n﹣1)d=4+(n﹣1)×(﹣1)=5﹣n.
(2)解:∵等差数列{an}中,a1=4,d=﹣1,an=5﹣n,
∴Sn= ![]() =
= ![]()
=﹣ ![]() =﹣
=﹣ ![]()
∵n∈N*,
∴n=4或n=5时,Sn取最大值10.
【解析】(1)设数列{an}公差为d,利用等差数列通项公式列出方程组,求出首项和公差,由此能求出{an}的通项公式.(2)由等差数列{an}中,a1=4,d=﹣1,an=5﹣n,求出Sn,利用配方法能求出n=4或n=5时,Sn取最大值10.
【考点精析】通过灵活运用等差数列的通项公式(及其变式)和等差数列的前n项和公式,掌握通项公式:![]() 或
或![]() ;前n项和公式:
;前n项和公式:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=( )
A.5
B.9
C.log345
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x﹣1|<2},B={x|x2﹣2mx+m2﹣1<0}.
(1)当m=3时,求A∩B;
(2)若A∪B=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5. 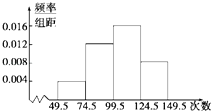
(1)求第四小组的频率;
(2)参加这次测试的学生人数是多少?
(3)在这次测试中,学生跳绳次数的中位数落在第几小组内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(m,cos2x),
=(m,cos2x), ![]() =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= ![]()
![]() ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2).
,﹣2).
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( ) 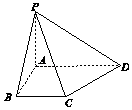
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 . 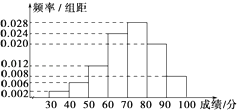
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 25 | a | b |
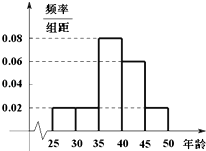
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com