
分析 甲乙从中任选一条共有15×15=225种不同取法,正方体6个面的中心构成一个正八面体,利用列举法求出两条直线互相垂直的情况,由此能求出所得的两条直线互相垂直的概率.
解答 解:如图所示,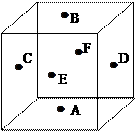
甲从这6个点中任意选两个点连成直线,共有C62=15条,乙也从这6个点中任意选两个点连成直线,共有C62=15条,
甲乙从中任选一条共有15×15=225种不同取法,
因正方体6个面的中心构成一个正八面体,
两条直线互相垂直的情况有:
AB⊥EF,AB⊥CD,EF⊥CD,有3组,
故所得的两条直线互相垂直的概率P=$\frac{3}{225}$=$\frac{1}{75}$.
故答案为:$\frac{1}{75}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 正数 | B. | 负数 | C. | 零 | D. | 不能确定符号 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin x | B. | -cos x | C. | sin x | D. | cos x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 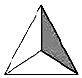 | B. | 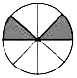 | C. | 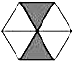 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
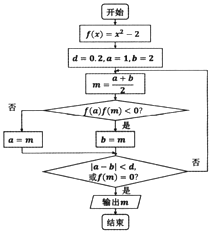
| A. | $\frac{11}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{23}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | 15 | C. | -3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com