
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,
,![]() ,
,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() .证明:
.证明:![]() ;
;
(3)若![]() 为等比数列,
为等比数列,![]() ,
,![]() ,求满足
,求满足![]() 的
的![]() 值.
值.
【答案】(1)![]() (2)见解析(3)1和2.
(2)见解析(3)1和2.
【解析】试题分析:
(1)由递推公式可得数列![]() 是以1为首项,2为公差的等差数列.故
是以1为首项,2为公差的等差数列.故![]() 的通项公式为
的通项公式为![]() .
.
(2)由题意,证得![]() 即可证得结论; 据此可得
即可证得结论; 据此可得![]() .
.
且![]() ,所以
,所以![]() .
.
故满足条件的![]() 的值为1和2.
的值为1和2.
试题解析:
解:(1) 由![]() ,得
,得![]() ,
,
即![]() ,所以
,所以![]() .
.
由![]() ,
,![]() ,可知
,可知![]() .
.
所以数列![]() 是以1为首项,2为公差的等差数列.
是以1为首项,2为公差的等差数列.
故![]() 的通项公式为
的通项公式为![]() .
.
(2)证法一:设数列![]() 的公差为
的公差为![]() ,则
,则![]() ,
,
由(1)知,![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() 恒成立,
恒成立,
所以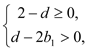 即
即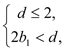
又由![]() ,得
,得![]() ,
,
所以![]()
![]()
![]()
![]() .
.
所以![]() ,得证.
,得证.
证法二:设![]() 的公差为
的公差为![]() ,假设存在自然数
,假设存在自然数![]() ,使得
,使得![]() ,
,
则![]()
![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() .
.
所以![]()
![]() ,
,
因为![]() ,所以存在
,所以存在![]() ,当
,当![]() 时,
时,![]() 恒成立.
恒成立.
这与“对任意的![]() ,都有
,都有![]() ”矛盾!
”矛盾!
所以![]() ,得证.
,得证.
(3)由(1)知,![]() .因为
.因为![]() 为等比数列,且
为等比数列,且![]() ,
,![]() ,
,
所以![]() 是以1为首项,3为公比的等比数列.
是以1为首项,3为公比的等比数列.
所以![]() ,
,![]() .
.
则![]()
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
而![]() ,所以
,所以![]() ,即
,即![]() (*).
(*).
当![]() 时,(*)式成立;
时,(*)式成立;
当![]() 时,设
时,设![]() ,
,
则![]()
![]() ,
,
所以![]() .
.
故满足条件的![]() 的值为1和2.
的值为1和2.


科目:高中数学 来源: 题型:
【题目】△ABC中,A、B、C的对边分别为a,b,c,面积为S,满足S= ![]() (a2+b2﹣c2).
(a2+b2﹣c2).
(1)求C的值;
(2)若a+b=4,求周长的范围与面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(m≥0)满足x=3﹣ ![]() (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a,b,c.角A,B,C成等差数列.
(1)求cosB的值;
(2)边a,b,c成等比数列,求sinAsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an},其前n项和Sn满足6Sn=an2+3an+2,且a1 , a2 , a6是等比数列{bn}的前三项.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1b1+a2b2+…+anbn , n∈N*,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2 ![]() ,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=
,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO= ![]() .
. 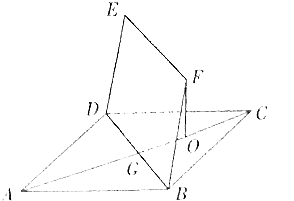
(1)求BF与平面ABCD所成的角的正切值;
(2)求三棱锥O﹣ADE的体积;
(3)求证:平面AEF⊥平面BCF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com