
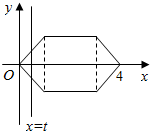
 如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6
如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6分析 (1)由题意可得等腰直角三角形的直角边为$\sqrt{2}$,斜边的中线(高)为1,分0<t≤1和1<t≤3以及3<t≤4,由三角形和矩形的面积公式可得;
(2)由(1)可得g(t)的解析式,结合二次函数的值域分类讨论可得.
解答 解:(1)由题意可得等腰直角三角形的直角边为$\sqrt{2}$,斜边的中线(高)为1,
∴当0<t≤1时,S=$\frac{1}{2}$($\sqrt{2}$t)2=t2;
当1<t≤3时,S=$\frac{1}{2}$($\sqrt{2}$)2+2(t-1)=2t-1;
当3<t≤4时,S=$\frac{1}{2}$($\sqrt{2}$)2+2×2+1-$\frac{1}{2}$[$\sqrt{2}$(4-t)]2=-t2+8t-10;
∴S=f(t)=$\left\{\begin{array}{l}{{t}^{2},0<t≤1}\\{2t-1,1<t≤3}\\{-{t}^{2}+8t-10,3<t≤4}\end{array}\right.$;
(2)由(1)可得$g(t)=\frac{f(t)}{t^2}$=$\left\{\begin{array}{l}{1,0<t≤1}\\{\frac{2t-1}{{t}^{2}},1<t≤3}\\{\frac{-{t}^{2}+8t-10}{{t}^{2}},3<t≤4}\end{array}\right.$,
当0<t≤1时,g(t)=1;
当1<t≤3时,g(t)=$\frac{2t-1}{{t}^{2}}$=$\frac{2}{t}$-$\frac{1}{{t}^{2}}$=-($\frac{1}{t}$-1)2+1,
∵1<t≤3,∴$\frac{1}{3}$≤$\frac{1}{t}$<1,故g(t)<g(1)=1;
当3<t≤4时,g(t)=$\frac{-{t}^{2}+8t-10}{{t}^{2}}$=-10($\frac{1}{t}$)2+8($\frac{1}{t}$)-1,
∵3<t≤4,∴$\frac{1}{4}$≤$\frac{1}{t}$<$\frac{1}{3}$,故g(t)<g(3)=$\frac{5}{9}$;
综上可得函数的最大值为1
点评 本题考查函数解析式的求解,涉及分段函数和二次函数的最值,属中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
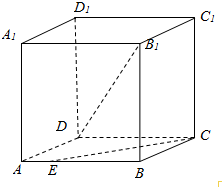 如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.
如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
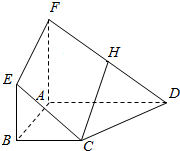 如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.
如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com