
【题目】如图,直三棱柱![]() 的底面是边长为2的正三角形,
的底面是边长为2的正三角形,![]() 分别是
分别是![]() 的中点。
的中点。
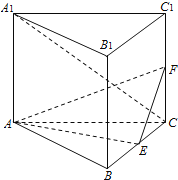
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】见解析
【解析】
试题分析:(1)证明面面垂直,实质是证明线面垂直,由题意可转化为证明![]() 平面
平面![]() ,而证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与证明往往需要结合平几知识,如本题利用正三角形性质得
,而证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与证明往往需要结合平几知识,如本题利用正三角形性质得![]() ,而由直三棱柱性质可推导得
,而由直三棱柱性质可推导得![]() (2)先根据线面垂直确定线面角:设AB的中点为D,证明
(2)先根据线面垂直确定线面角:设AB的中点为D,证明![]() 平面
平面![]() ,则直线
,则直线![]() 直线
直线![]() 与平面
与平面![]() 所成的角,由直三棱柱性质易得三棱锥
所成的角,由直三棱柱性质易得三棱锥![]() 的高
的高![]() ,最后根据三棱锥体积公式求体积.
,最后根据三棱锥体积公式求体积.
试题解析:(I)如图,因为三棱柱![]() 是直三棱柱,
是直三棱柱,
所以![]() ,又
,又![]() 是正三角形
是正三角形![]() 的边
的边![]() 的中点,
的中点,
所以![]() ,因此
,因此![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() 。
。
(2)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,因为
,因为![]() 是正三角形,所以
是正三角形,所以![]() ,又三棱柱
,又三棱柱![]() 是直三棱柱,所以
是直三棱柱,所以![]() ,因此
,因此![]() 平面
平面![]() ,于是
,于是![]() 直线
直线![]() 与平面
与平面![]() 所成的角,由题设知
所成的角,由题设知![]() ,
,
所以![]()
![]()
在![]() 中,
中,![]() ,所以
,所以![]()
故三棱锥![]() 的体积
的体积![]() .
.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】类比平面几何中的命题:“垂直于同一直线的两条直线平行”,在立体几何中,可以得到命题“__________”,这个类比命题的真假性是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法,正确的个数是
①若两直线的倾斜角相等,则它们的斜率也一定相等;
②一条直线的倾斜角为30°;
③倾斜角为0°的直线只有一条;
④直线的倾斜角α的集合{α|0°≤α<180°}与直线集合建立了一一对应关系.
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)求![]() 的极值;
的极值;
(2)设![]() ≤
≤![]() ,记
,记![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)设函数![]() (
(![]() 为常数),若使
为常数),若使![]() ≤
≤![]() ≤
≤![]() 在
在![]() 上恒成立的实数
上恒成立的实数![]() 有且只有一个,求实数
有且只有一个,求实数![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国乒乓球队备战里约奥运会热身赛暨选拔赛于2016年7月14日在山东威海开赛.种子选手![]() 与
与![]() ,
,![]() ,
,![]() 三位非种子选手分别进行一场对抗赛,按以往多次比赛的统计,
三位非种子选手分别进行一场对抗赛,按以往多次比赛的统计,![]() 获胜的概率分别为
获胜的概率分别为![]() ,
,![]() ,
,![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(1)若![]() 至少获胜两场的概率大于
至少获胜两场的概率大于![]() ,则
,则![]() 入选征战里约奥运会的最终大名单,否则不予入选,问
入选征战里约奥运会的最终大名单,否则不予入选,问![]() 是否会入选最终的大名单?
是否会入选最终的大名单?
(2)求![]() 获胜场数
获胜场数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com