
【题目】已知函数 在点M(1,f(1))处的切线方程为
在点M(1,f(1))处的切线方程为![]()
求(1)实数a,b的值;
(2)函数![]() 的单调区间及在区间[0,3]上的最值.
的单调区间及在区间[0,3]上的最值.
【答案】(1)a=b=4(2)4, ![]()
【解析】试题分析:(1)根据切线方程求出切线的斜率,可得到切点坐标,求出函数的导数,利用导函数值与斜率关系,即可列方程求出![]() 的值;(2)求出
的值;(2)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间,根据单调性可得函数的极值,比较极值与区间端点值的函数值可求解闭区间的函数的最值.
的减区间,根据单调性可得函数的极值,比较极值与区间端点值的函数值可求解闭区间的函数的最值.
试题解析:(1)因为在点M(1,f(1))处的切线方程为9x+3y﹣10=0,
所以切线斜率是k=﹣3
且9×1+3f(1)﹣10=0,
求得![]() ,即点
,即点![]() 又函数
又函数![]() ,则f′(x)=x2﹣a所以依题意得
,则f′(x)=x2﹣a所以依题意得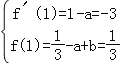 解得
解得![]()
(2)由(1)知![]()
所以f′(x)=x2﹣4=(x+2)(x﹣2)令f′(x)=0,解得x=2或x=﹣2
当f′(x)>0x>2或x<﹣2;当f′(x)<0﹣2<x<2
所以函数f(x)的单调递增区间是(﹣∞,2),(2,+∞)
单调递减区间是(﹣2,2)又x∈[0,3]
所以当x变化时,f(x)和f′(x)变化情况如下表:
X | 0 | (0,2) | 2 | (2,3) | 3 |
f′(x) | ﹣ | 0 | + | 0 | |
f(x) | 4 | ↘ | 极小值 | ↗ | 1 |
所以当x∈[0,3]时,f(x)max=f(0)=4,
![]()


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】某高三毕业班甲、乙两名同学在连续的8次数学周练中,统计解答题失分的茎叶图如下: 
(1)比较这两名同学8次周练解答题失分的均值和方差的大小,并判断哪位同学做解答题相对稳定些;
(2)以上述数据统计甲、乙两名同学失分超过15分的频率作为频率,假设甲、乙两名同学在同一次周练中失分多少互不影响,预测在接下来的2次周练中,甲、乙两名同学失分均超过15分的次数X的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆锥PO中,已知![]() ,圆O的直径
,圆O的直径![]() ,C是弧AB的中点,D为AC的中点.
,C是弧AB的中点,D为AC的中点.

(1)求异面直线PD和BC所成的角的正切值;
(2)求直线OC和平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过A(-4,0),B(1,5),C(6,0)三点.
(Ⅰ)求圆M的方程
(Ⅱ)若直线ax-y+5=0(a>0)与圆M相交于P,Q两点,是否存在实数a,使得弦PQ的垂直平分线l过点E(-2,4),若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a+1)lnx+ ![]() x2(a<﹣1)对任意的x1、x2>0,恒有|f(x1)﹣f(x2)|≥4|x1﹣x2|,则a的取值范围为 .
x2(a<﹣1)对任意的x1、x2>0,恒有|f(x1)﹣f(x2)|≥4|x1﹣x2|,则a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一段演绎推理是这样的: “直线平行于平面,则平行于平面内所有直线;已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线
∥直线![]() ”的结论显然是错误的,这是因为( )
”的结论显然是错误的,这是因为( )
A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 非以上错误
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com