
分析 根据不等式进行化简,求出不等式对应的解集,根据区间长度的定义进行求解即可.
解答 解:∵$\frac{1}{x-a}+\frac{1}{x-b}≥1$,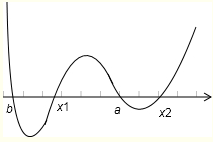
∴$\frac{2x-(a+b)}{(x-a)(x-b)}$≥1,
即$\frac{2x-(a+b)}{(x-a)(x-b)}$-1≥0,则$\frac{{x}^{2}-(2+a+b)x+ab+a+b}{(x-a)(x-b)}$≤0,
设x2-(2+a+b)x+ab+a+b=0的根为x1和x2.
则有求根公式得x1=$\frac{a+b+2-\sqrt{(a-b)^{2}+4}}{2}$∈(a,b),
x2=$\frac{a+b+2+\sqrt{(a-b)^{2}+4}}{2}$>a,
x1+x2═2+a+b,
则由穿根法得不等式的解集为[b,x1]∪[a-x2],
则构成的区间的长度之和x1-b+x2-a=x1-x2-a-b=2+a+b-a-b=2,
故答案为:2
点评 本题主要考查区间长度的定义,利用穿根法求出不等式的解集是解决本题的关键.


科目:高中数学 来源: 题型:填空题
 如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.
如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 345° | B. | 375° | C. | -$\frac{11}{12}$π | D. | $\frac{23}{12}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com