练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四棱锥中，平面平面，为等边三角形，，，，点是的中点.

    （1）求证：平面；

    （2）求二面角的余弦值.

    【答案】（1）证明见解析（2）

    【解析】

    （1）取中点，连结，，证明四边形为平行四边形得到答案.

    （2）证明平面，如图建立空间直角坐标系，平面的法向量，面的法向量，计算夹角得到答案.

    （1）取中点，连结，.

    因为为中点，所以，.

    因为，.所以且.

    所以四边形为平行四边形，所以.

    因为平面，平面，

    所以平面.

    （2）取中点，连结.因为，所以.

    因为平面平面，平面平面，平面，

    所以平面，取中点，连结，

    则.以为原点，如图建立空间直角坐标系，

    由，则，，，，，

    ，.平面的法向量，

    设平面的法向量，由，得.

    令，则，.由图可知，

    二面角是锐二面角，所以二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】推进垃圾分类处理，是落实绿色发展理念的必然选择，也是打赢污染防治攻坚战的重要环节．为了解居民对垃圾分类的了解程度某社区居委会随机抽取1000名社区居民参与问卷测试，并将问卷得分绘制频率分布表如表：

    得分

    [30，40）

    [40，50）

    [50，60）

    [60，70）

    [70，80）

    [80，90）

    [90，100]

    男性人数

    40

    90

    120

    130

    110

    60

    30

    女性人数

    20

    50

    80

    110

    100

    40

    20

    （1）从该社区随机抽取一名居民参与问卷测试试估计其得分不低于60分的概率：

    （2）将居民对垃圾分类的了解程度分为“比较了解”（得分不低于60分）和“不太了解”（得分低于60）两类，完成2×2列联表，并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关？

    不太了解

    比较了解

    合计

    男性

    女性

    合计

    （3）从参与问卷测试且得分不低于80分的居民中，按照性别进行分层抽样，共抽取10人，现从这10人中随机抽取3人作为环保宣传队长，设3人中男性队长的人数为，求的分布列和期望．

    附：．

    临界值表：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数,若存在区间,使得,则称函数为“可等域函数”,区间A为函数的一个“可等域区间”.给出下列四个函数:①;②;③;④.其中存在唯一“可等域区间”的“可等域函数”的个数是( )

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥中，平面平面， 则三棱锥的外接球的表面积为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知ABCD为梯形，AB∥CD，CD=2AB，M为线段PC上一点.

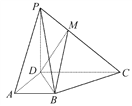
    (1)设平面PAB∩平面PDC=l，证明：AB∥l；

    (2)在棱PC上是否存在点M，使得PA∥平面MBD，若存在，请确定点M的位置；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且椭圆上一点与椭圆的两个焦点构成的三角形周长为．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设直线与椭圆交于，两点，且以为直径的圆过椭圆的右顶点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市坚持农业与旅游融合发展，着力做好旅游各要素，完善旅游业态，提升旅游接待能力.为了给游客提供更好的服务，旅游部门需要了解游客人数的变化规律，收集并整理了年月至年月期间月接待游客量(单位：万人)的数据，绘制了如图所示的折线图.根据该折线图，下列结论正确的是（ ）

    A.月接待游客量逐月增加

    B.年接待游客量逐年增加

    C.各年的月接待游客量高峰期大致在7，8月

    D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”，主要指德育；“乐”，主要指美育；“射”和“御”，就是体育和劳动；“书”，指各种历史文化知识；“数”，指数学.某校国学社团开展“六艺”课程讲座活动，每艺安排一节，连排六节，一天课程讲座排课有如下要求：“数”必须排在第三节，且“射”和“御”两门课程相邻排课，则“六艺”课程讲座不同的排课顺序共有（ ）

    A.12种B.24种C.36种D.48种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的定义域为，若存在区间使得：

    （Ⅰ）在上是单调函数；

    （Ⅱ）在上的值域是，

    则称区间为函数的“倍值区间”．

    下列函数中存在“倍值区间”的有______________（填上所有你认为正确的序号）

    ①； ②；

    ③； ④．

    查看答案和解析>>

    同步练习册答案