练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若等比数列{an}的前n项和Sn=2016n+t（t为常数），则a1的值为（ ）
    A.2013
    B.2014
    C.2015
    D.2016

    【答案】C
    【解析】解：∵等比数列{an}的前n项和Sn=2016n+t（t为常数），
    ∴ +t=2016+t，
    a2=S2﹣S1=20162+t﹣（2016+t）=4062240，
    a3=S3﹣S2=20163+t﹣（20162+t）=8189475840，
    ∵ ，
    ∴40622402=（2016+t）×8189475840，
    解得t=﹣1，
    ∴a1=2016+（﹣1）=2015．
    故选：C．
    【考点精析】本题主要考查了等比数列的前n项和公式的相关知识点，需要掌握前项和公式：才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= + ，则下列命题中正确命题的序号是 ．
    ①f（x）是偶函数；
    ②f（x）的值域是[ ，2]；
    ③当x∈[0， ]时，f（x）单调递增；
    ④当且仅当x=2kπ± （k∈Z）时，f（x）= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求曲线在点处的切线方程；

    （2）求函数的单调区间及极值；

    （3）对， 成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4:坐标系与参数方程

    在平面直角坐标系中，直线经过点，倾斜角为.在以原点为极点， 轴正半轴为极轴的极坐标系中，曲线的方程为.

    （1）写出直线的参数方程和曲线的直角坐标方程；

    （2）设直线与曲线相交于两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， （其中， ），且函数的图象在点处的切线与函数的图象在点处的切线重合．

    （1）求实数， 的值；

    （2）记函数，是否存在最小的正常数，使得当时，对于任意正实数，不等式恒成立？给出你的结论，并说明结论的合理性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如：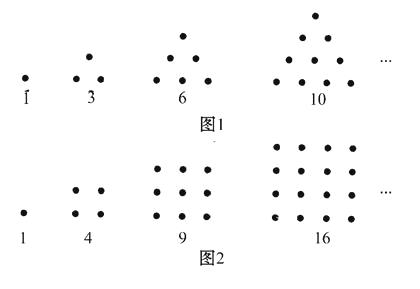
    他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似地，称图2中的1，4，9，16，…，这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
    A.289
    B.1024
    C.1225
    D.1378

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和Sn=n2﹣n，数列{bn}的前n项和Tn=4﹣bn ．
    （1）求数列{an}和{bn}的通项公式；
    （2）设cn= anbn ， 求数列{cn}的前n项和Rn的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面是正方形，每条侧棱的长都是底面边长的倍，为侧棱上的点．

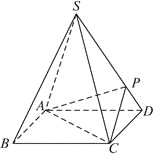
    （1）求证：．

    （2）若⊥平面，求二面角的大小．

    （3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC?若存在，求SE∶EC的值；若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： （）的离心率为，直线： 与以原点为圆心、椭圆的短半轴长为半径的圆相切.

    （1）求椭圆的方程；

    （2）过椭圆的左顶点作直线，与圆相交于两点， ，若是钝角三角形，求直线的斜率的取值范围.

    查看答案和解析>>

    同步练习册答案