
【题目】设函数![]() 是偶函数.
是偶函数.
(1)若不等式![]() 对任意实数
对任意实数![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若
,若![]() 在
在![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为![]() 的调查样本,其中城镇户籍与农民户籍各
的调查样本,其中城镇户籍与农民户籍各![]() 人;男性
人;男性![]() 人,女性
人,女性![]() 人.绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
人.绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
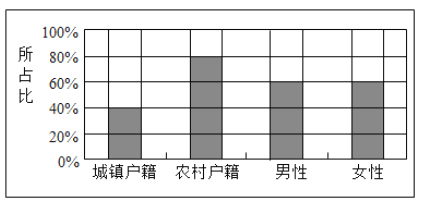
A.是否倾向选择生育二胎与户籍有关
B.是否倾向选择生育二胎与性别无关
C.倾向选择生育二胎的人员中,男性人数与女性人数相同
D.倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①A=![]() 的子集有
的子集有![]() 个;
个;
②命题“![]() ”的否定是“
”的否定是“![]() 使得
使得![]() ”;
”;
③“![]() ”是“函数
”是“函数![]() 取得最大值”的充分不必要条件;
取得最大值”的充分不必要条件;
④根据对数定义,对数式![]() 化为指数式
化为指数式![]() ;
;
⑤若![]() ,则
,则![]() 的取值范围为
的取值范围为![]() ;
;
⑥![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
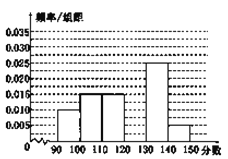
(1)求分数在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,试探究:直线
,试探究:直线![]() 是否过定点,若是,求该定点的坐标,若不是,请说明.
是否过定点,若是,求该定点的坐标,若不是,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅱ)若![]() ,方程
,方程![]() 至少有两个不等的解,求
至少有两个不等的解,求![]() 的取值集合;
的取值集合;
(Ⅲ)若函数![]() 为
为![]() 上的单调减函数,
上的单调减函数,
①求![]() 的取值范围;
的取值范围;
②若不等式![]() 成立,求实数
成立,求实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市实施全域旅游,将乡村旅游公路建设与特色田园乡村发展结合,精心打造全长365公里的“1号公路”,对内串联区域内主要景区景点和自然村,对外通达周边县(市),以路引景、为景串线,形成一个“大环小圈、内连外引”的路网体系.如今的“1号公路”,不仅成为该市旅游业的“颜值担当”,更成为推动乡村振兴的“实力担当”,农村居住环境日益改善,新农村别墅随处可见.图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面
市实施全域旅游,将乡村旅游公路建设与特色田园乡村发展结合,精心打造全长365公里的“1号公路”,对内串联区域内主要景区景点和自然村,对外通达周边县(市),以路引景、为景串线,形成一个“大环小圈、内连外引”的路网体系.如今的“1号公路”,不仅成为该市旅游业的“颜值担当”,更成为推动乡村振兴的“实力担当”,农村居住环境日益改善,新农村别墅随处可见.图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面![]() 和
和![]() 是全等的等腰梯形,左右两坡屋面
是全等的等腰梯形,左右两坡屋面![]() 和
和![]() 是全等的三角形.点
是全等的三角形.点![]() 在平面
在平面![]() 和
和![]() 上的射影分别为
上的射影分别为![]() (即:
(即:![]() 平面
平面![]() ,垂足为
,垂足为![]() ;
;![]() ,垂足为
,垂足为![]() ).已知
).已知![]() ,梯形
,梯形![]() 的面积是
的面积是![]() 面积的2.2倍.
面积的2.2倍.![]() .
.

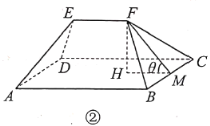
(1)当![]() 时,求屋顶面积的大小;
时,求屋顶面积的大小;
(2)求屋顶面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)已知上部屋顶造价与屋顶面积成正比,比例系数为![]() (
(![]() 为正的常数),下部主体造价与其高度成正比,比例系数为
为正的常数),下部主体造价与其高度成正比,比例系数为![]() .现欲造一栋上、下总高度为
.现欲造一栋上、下总高度为![]() 的别墅,试问:当
的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com