
分析 (1)化简集合A,求出a=2时集合B,再计算A∩B和A∪B;
(2)求出CRA,根据(∁RA)∩B=B得出B⊆(∁RA),
讨论B=∅和B≠∅时,求出实数a的取值范围.
解答 解:A={x|2x2-7x+3≤0}={x|$\frac{1}{2}$≤x≤3},B={x||x|<a};
(1)当a=2时,B={x|-2<x<2},
∴A∩B={x|$\frac{1}{2}$≤x<2},
A∪B={x|-2<x≤3};
(2)∵∁RA={x|x<$\frac{1}{2}$或x>3},
且(∁RA)∩B=B,
即B⊆(∁RA);
当B=∅时,a≤0,满足题意;
当B≠∅时,a>0,
此时B={x|-a<x<a},
应满足0$<a<\frac{1}{2}$;
综上,实数a的取值范围是a<$\frac{1}{2}$.
点评 本题考查了集合的化简与运算问题,是综合性题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{x}$ | B. | $y=\frac{1}{{\sqrt{x}}}$ | C. | $y=\frac{1}{x}$ | D. | y=x2+x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -1 | C. | 2或-1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
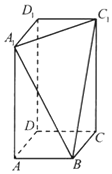 长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$
长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com