
【题目】底面为菱形的直棱柱![]()
中, ![]()
分别为棱![]()
的中点.
(1)在图中作一个平面![]()
,使得![]()
,且平面![]()
.(不必给出证明过程,只要求作出![]()
与直棱柱![]()
的截面).
(2)若![]()
,求平面![]()
与平面![]()
的距离![]()
.
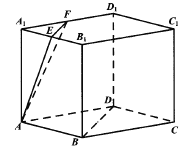
【答案】(1)见解析;(2)![]()
.
【解析】试题分析:(1)作面面平行,实质作线线平行,而线线平行的寻找往往利用平几知识,如三角形中位线、平行四边形性质等,本题中已有![]()
,根据对称性在平面![]()
中寻找另一组平行线,(2)利用向量投影可求两平面之间距离,先根据条件建立恰当直角坐标系,设立各点坐标,解方程组得平面![]()
的法向量![]()
,利用向量数量积求向量![]()
在![]()
方向上投影的绝对值,即为平面![]()
与平面![]()
的距离![]()
.
试题解析:
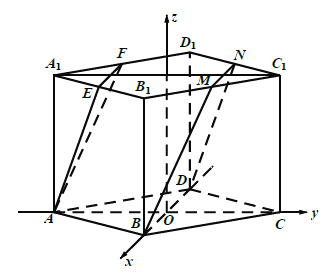
(1)如图,取![]()
的中点![]()
,连接![]()
,则平面![]()
即为所求平面![]()
.
(2)如图,连接![]()
交![]()
于![]()
,
∵在直棱柱![]()
中,底面为菱形,
∴![]()
,
∴分别以![]()
为![]()
轴, ![]()
为原点建立如图所示空间直角坐标系,
又∵所有棱长为2, ![]()
,
∴![]()
, ![]()
, ![]()
,
∴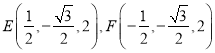
,
∴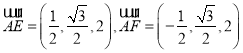
, ![]()
,
设![]()
是平面![]()
的一个法向量,则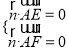
,即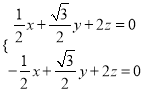
,
令![]()
得![]()
, ![]()
,
∴点![]()
到平面![]()
的距离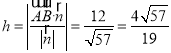
,
∴平面![]()
与平面![]()
的距离![]()
.


科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
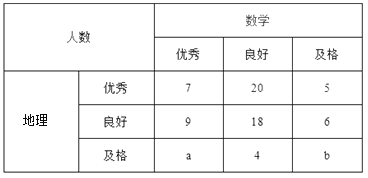
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() .
.
(Ⅰ)若在该样本中,数学成绩优秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·桂林高二检测)如图所示,在四边形ABCD中,AB=AD=CD=1,BD=![]() ,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.

(1)A′C⊥BD.(2)∠BA′C=90°.
(3)CA′与平面A′BD所成的角为30°.
(4)四面体A′-BCD的体积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2014陕西理8】原命题为“若![]() 互为共轭复数,则
互为共轭复数,则![]() ”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
A. 真,假,真 B. 假,假,真
C. 真,真,假 D. 假,假,假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过原点的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆上不同于
为椭圆上不同于![]() 的一点,直线
的一点,直线![]() 的斜率均存在,且直线
的斜率均存在,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设![]() 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为![]() 的直线
的直线![]() 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于![]() 两点.若点
两点.若点![]() 在以
在以![]() 为直径的圆内部,求
为直径的圆内部,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,求|a+b|和a+b与c的夹角;
(2)设O为△ABC的外心,已知AB=3,AC=4,非零实数x,y满足![]() =x
=x![]() +y
+y![]() ,且x+2y=1,求cos ∠BAC的值.
,且x+2y=1,求cos ∠BAC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每个月可卖出
元,每个月可卖出![]() 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨![]() 元,则每个月少卖
元,则每个月少卖![]() 件(每件售价不能高于
件(每件售价不能高于![]() 元).设每件商品的售价上涨
元).设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com