
【题目】20世纪70年代,流行一种游戏——角谷猜想,规则如下:任意写出一个自然数![]() ,按照以下的规律进行变换,如果
,按照以下的规律进行变换,如果![]() 是奇数,则下一步变成
是奇数,则下一步变成![]() ;如果
;如果![]() 是偶数,则下一步变成
是偶数,则下一步变成![]() ,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,下列程序框图就是根据这个游戏而设计的,如果输出的
,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,下列程序框图就是根据这个游戏而设计的,如果输出的![]() 的值为6,则输入的
的值为6,则输入的![]() 值可以为( )
值可以为( )
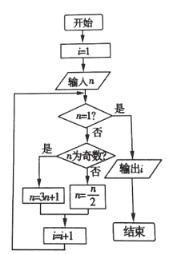
A. 5或16B. 16C. 5或32D. 4或5或32
【答案】C
【解析】
根据各个选项n的值,模拟程序的运行,依次验证程序的输出的i的值是否为6即可得解.
模拟程序的运行,由题意可得
当输入的n的值为5时,
i=1,第1次循环,n=5,n为奇数,n=16
i=2,第2次循环,n为偶数,n=8
i=3,第3次循环,n为偶数,n=4
i=4,第4次循环,n为偶数,n=2
i=5,第5次循环,n为偶数,n=1
i=6,满足条件n=1,退出循环,输出i的值为6.符合题意.
当输入的n的值为16时,
i=1,第1次循环,n=16,n为偶数,n=8
i=2,第2次循环,n为偶数,n=4
i=3,第3次循环,n为偶数,n=2
i=4,第4次循环,n为偶数,n=1
i=5,满足条件n=1,退出循环,输出i的值为5.不符合题意.
当输入的n的值为32时,
i=1,第1次循环,n=32,n为偶数,n=16
i=2,第2次循环,n为偶数,n=8
i=3,第3次循环,n为偶数,n=4
i=4,第4次循环,n为偶数,n=2
i=5,第5次循环,n为偶数,n=1
i=6,满足条件n=1,退出循环,输出i的值为6.符合题意.
当输入的n的值为4时,
i=1,第1次循环,n=4,n为偶数,n=2
i=2,第2次循环,n为偶数,n=1
i=3,满足条件n=1,退出循环,输出i的值为3.不符合题意.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,设直线![]() :
:![]() ,
,![]() :
:![]() .点
.点![]() 的坐标为
的坐标为![]() .过点
.过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且与
,且与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (
(![]() ,
,![]() 的纵坐标均为正数).
的纵坐标均为正数).
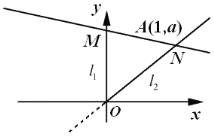
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,求
,求![]() 面积的最小值;
面积的最小值;
(3)是否存在实数![]() ,使得
,使得![]() 的值与
的值与![]() 无关?若存在,求出所有这样的实数
无关?若存在,求出所有这样的实数![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
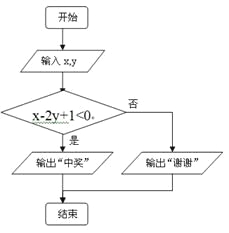
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,已知其离心率为
,已知其离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的标准方程.
(2)设![]() ,
,![]() 是椭圆上位于
是椭圆上位于![]() 轴上方的两点,且直线
轴上方的两点,且直线![]() 与直线
与直线![]() 平行,
平行,![]() 与
与![]() 交于点
交于点![]() ,探究
,探究![]() 是否为定值?如果为定值,请求出该定值;如果不为定值,请说明理由.
是否为定值?如果为定值,请求出该定值;如果不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小威初三参加某高中学校的数学自主招生考试,这次考试由十道选择题组成.得分要求是:做对一道题得![]() 分,做错一道题扣去
分,做错一道题扣去![]() 分,不做得
分,不做得![]() 分,总得分
分,总得分![]() 分就算及格.小威的目标是至少得
分就算及格.小威的目标是至少得![]() 分获得及格.在这次考试中,小威确定他做的前六题全对,记
分获得及格.在这次考试中,小威确定他做的前六题全对,记![]() 分;而他做余下的四道题中每道题做对的概率均为
分;而他做余下的四道题中每道题做对的概率均为![]() .考试中,小威思量:从余下的四道题中再做一道并且及格的概率
.考试中,小威思量:从余下的四道题中再做一道并且及格的概率![]() ;从余下的四道题中恰做两道并且及格的概率
;从余下的四道题中恰做两道并且及格的概率![]() .他发现
.他发现![]() ,只做一道更容易及格.
,只做一道更容易及格.
(1)求:小威从余下的四道题中恰做三道并且及格的概率![]() ,从余下的四道题中全做并且及格的概率
,从余下的四道题中全做并且及格的概率![]() ,求
,求![]() 及
及![]() ;
;
(2)由于![]() 的大小影响,请你帮小威讨论:小威从余下的四道题中恰做几道并且及格的概率最大?
的大小影响,请你帮小威讨论:小威从余下的四道题中恰做几道并且及格的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,如果![]() 与
与![]() 都是整数,就称点
都是整数,就称点![]() 为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
①存在这样的直线,既不与坐标轴平行又不经过任何整点
②如果![]() 与
与![]() 都是无理数,则直线
都是无理数,则直线![]() 不经过任何整点
不经过任何整点
③直线![]() 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当![]() 经过两个不同的整点
经过两个不同的整点
④直线![]() 经过无穷多个整点的充分必要条件是:
经过无穷多个整点的充分必要条件是:![]() 与
与![]() 都是有理数
都是有理数
⑤存在恰经过一个整点的直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com