
设函数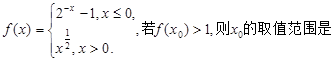 ( )
( )
| A.(-1,1) | B.(-1,+ ) ) |
C. | D. |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
具有性质: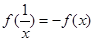 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:① ;②
;②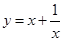 ;③
;③ 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )
| A.①② | B.①③ | C.②③ | D.只有① |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为 ,值域为{1,7}的“孪生函数”共有 ( )
,值域为{1,7}的“孪生函数”共有 ( )
| A.10个 | B.9个 | C.8个 | D.4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)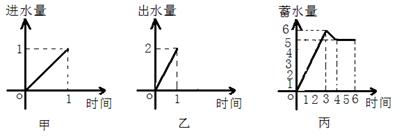
给出以下3个论断:①0点到3点只进水不出水;C②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
| A.0 | B. 1 | C. 2 | D. 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
对任意实数 ,定义运算
,定义运算 ,其中
,其中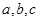 是常数,等式右边的运算是通常的加法和乘法运算。已知
是常数,等式右边的运算是通常的加法和乘法运算。已知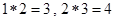 ,并且有一个非零常数
,并且有一个非零常数 ,使得对任意实数
,使得对任意实数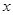 , 都有
, 都有 ,则
,则 的值是( )
的值是( )
A.- | B.4 | C.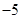 | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com