解:(1)x∈(0,2]时,-x∈[-2,0),则
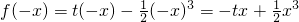
,
∵函数f(x)是定义在[-2,2]上的奇函数,即f(-x)=-f(x),
∴
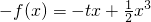
,即
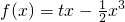
,又可知f(0)=0,
∴函数f(x)的解析式为
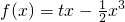
,x∈[-2,2];
(2)
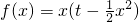
,∵t∈[2,6],x∈[-2,0],∴
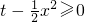
,f(x)<0
∵
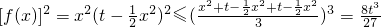
,∴
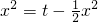
,
即
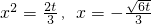
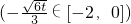
时,
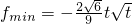
.
猜想f(x)在[0,2]上的单调递增区间为
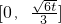
.
(3)t≥9时,任取-2≤x
1<x
2≤2,
∵
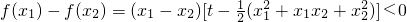
,
∴f(x)在[-2,2]上单调递增,即f(x)∈[f(-2),f(2)],
即f(x)∈[4-2t,2t-4],t≥9,∴4-2t≤-14,2t-4≥14,
∴14∈[4-2t,2t-4],∴当t≥9时,函数y=f(x)的图象上至少有一个点落在直线y=14上.
分析:(1)设x∈(0,2]?-x∈[-2,0)?
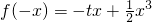
,由f(x)为奇函数可得f(-x)=-f(x),代入可求f(x)x∈(0,2];
由奇函数的性质可知f(0)=0,从而可得f(x) x∈[-2,2]
(2)由知
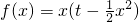
<0,x∈[-2,0],t∈[2,6]
利用平均值不等式可得,
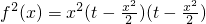
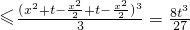
(当
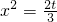
时取等号)
(3)利用单调性的定义(或导数法)判断函数在[-2,2]上单调性,从而确定函数的值域,然后证明14在值域内即可
点评:本题综合考查函数的解析式的求解、利用均值不等式求函数的最值、及利用定义或导数法判断函数的单调性,在利用均值不等式求最值时,要注意验证各项的符号及等号成立的条件.

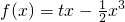 (t为常数).
(t为常数).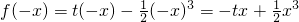 ,
,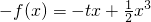 ,即
,即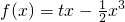 ,又可知f(0)=0,
,又可知f(0)=0,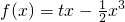 ,x∈[-2,2];
,x∈[-2,2];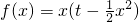 ,∵t∈[2,6],x∈[-2,0],∴
,∵t∈[2,6],x∈[-2,0],∴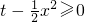 ,f(x)<0
,f(x)<0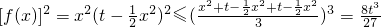 ,∴
,∴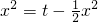 ,
,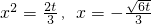
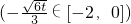 时,
时,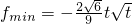 .
.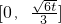 .
.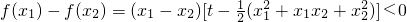 ,
,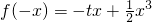 ,由f(x)为奇函数可得f(-x)=-f(x),代入可求f(x)x∈(0,2];
,由f(x)为奇函数可得f(-x)=-f(x),代入可求f(x)x∈(0,2];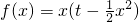 <0,x∈[-2,0],t∈[2,6]
<0,x∈[-2,0],t∈[2,6]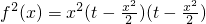
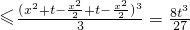 (当
(当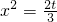 时取等号)
时取等号)

 已知函数f(x)=x+
已知函数f(x)=x+