设
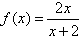
,x
1=1,x
n=f(x
n-1)(n≥2,n∈N*),
(Ⅰ)求x
2,x
3,x
4的值;
(Ⅱ)归纳{x
n}的通项公式,并用数学归纳法证明.
解:(Ⅰ)
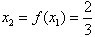
,
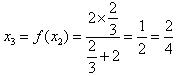
,
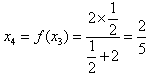
;
(Ⅱ)根据计算结果,可以归纳出
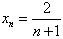
;
当n=1时,
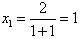
,与已知相符,归纳出的公式成立;
假设当n=k(k∈N*)时,公式成立,即
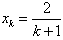
,
那么,
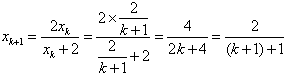
,
所以,当n=k+1时,公式也成立;
综上,
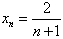
对于任何n∈N*都成立。
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
P
n(x
n,y
n)是函数y=x
2(x≥0)图象上的动点,以P
n为圆心的⊙P
n与x轴都相切,且⊙P
n与⊙P
n+1又彼此外切,若x
1=1,x
n+1<x
n.
(1)求证:数列
{}是等差数列;
(2)设⊙P
n的面积为S
n,求证:
++…+<.
查看答案和解析>>
科目:高中数学
来源:
题型:
设f(x)=
,x
1=1,x
n=f(x
n-1)(n≥2,n∈N
*).
(Ⅰ)求x
2,x
3,x
4的值;
(Ⅱ)归纳{x
n}的通项公式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列
{xn}满足:x1=1且xn+1=,n∈N*.
(1)计算x
2,x
3,x
4的值;
(2)试比较x
n与2的大小关系;
(3)设a
n=|x
n-2|,S
n为数列{a
n}前n项和,求证:当
n≥2时,Sn≤2-.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
设 ,x1=1,xn=f(xn-1)(n≥2,n∈N*).
,x1=1,xn=f(xn-1)(n≥2,n∈N*).
(Ⅰ)求x2,x3,x4的值;
(Ⅱ)归纳{xn}的通项公式,并用数学归纳法证明.
查看答案和解析>>

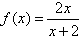 ,x1=1,xn=f(xn-1)(n≥2,n∈N*),
,x1=1,xn=f(xn-1)(n≥2,n∈N*), 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案